Enoncé du problème n° 3
Enoncé du problème n° 3
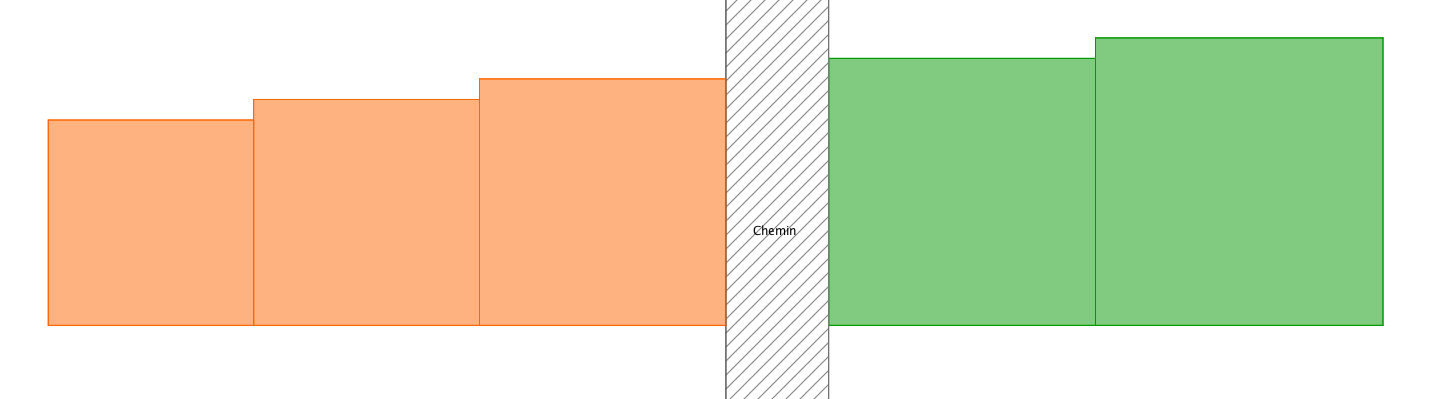
- Un père partage ses 5 terrains entre ses deux fils.
- Les cinq champs représentés ont pour côté des entiers consécutifs.
- Déterminer le côté de chacun de ces carrés sachant que le partage a été équitable.
Auteur : Luc GIRAUD
Correction du problème n° 3
Notons $x$ le côté du troisième carré.
Les carrés étant classés dans l'ordre croissat de mesure de longueur.
Les mesures dess côtés sont donc : $$x-2;x-1;x;x+1;x+2$$ Ces nombres étant des longueurs sont positifs, donc $x\geqslant 2$.
Le partage est équitable lorsque : $$\begin{array}{ rl} (x-2)^2+(x-1)^2+x^2=(x+1)^2(x+2)^2 &\iff x^2-4x+4+x^2-2x+1=x^2=x^2+2x+1+x^2+4x+4\\ &\iff x^2-12x =0\\ &\iff x(x-12)= 0\\ &\iff x=0 \text{ ou } x=12 \end{array} $$ Or $x\geqslant 2$; on ne retient donc que $x=12$.
Les carrés étant classés dans l'ordre croissat de mesure de longueur.
Les mesures dess côtés sont donc : $$x-2;x-1;x;x+1;x+2$$ Ces nombres étant des longueurs sont positifs, donc $x\geqslant 2$.
Le partage est équitable lorsque : $$\begin{array}{ rl} (x-2)^2+(x-1)^2+x^2=(x+1)^2(x+2)^2 &\iff x^2-4x+4+x^2-2x+1=x^2=x^2+2x+1+x^2+4x+4\\ &\iff x^2-12x =0\\ &\iff x(x-12)= 0\\ &\iff x=0 \text{ ou } x=12 \end{array} $$ Or $x\geqslant 2$; on ne retient donc que $x=12$.
Le premier fils aura donc 3 champs carrés de côtés respectifs 10;11;12.
Le deuxième fils aura 2 champs carrés de côtés 13 et 14.
On peut vérifier que : $$10^2+11^2+12^2=13^2+14^2=365$$
Le deuxième fils aura 2 champs carrés de côtés 13 et 14.
On peut vérifier que : $$10^2+11^2+12^2=13^2+14^2=365$$
D'autres problèmes ?

Problème n° 119

Problème n° 118

Problème n° 117

Problème n° 116

Problème n° 115

Problème n° 114

Problème n° 113

Problème n° 112

Problème n° 111



