Enoncé du problème n° 16
- Montrer que l'aire des quatre lunules égale l'aire du carré.
Auteur : Luc GIRAUD
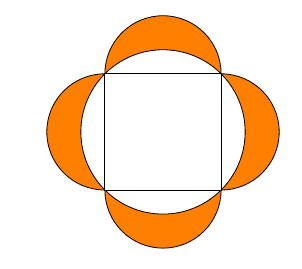
Correction du problème n°16
- Notons $\mathcal{A}$ l'aire totale formée par la figure. On décompose la figure totale de deux façons différentes.

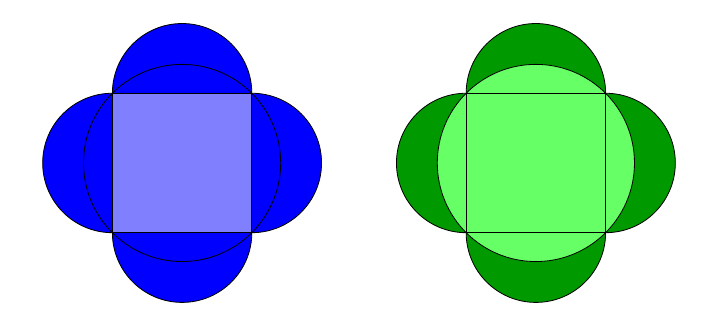
- Première façon, sur la figure de gauche. L'aire totale $\mathcal{A}$ se décompose en l'aire $\mathcal{A}_\text{carré}$ du carré (zone bleu clair, dont on veut calculer l'aire) et l'aire $\mathcal{A}_\text{demi-disques}$ formée par $4$ demi-disques (zone bleu foncé) : $$\mathcal{A} = \mathcal{A}_\text{carré} + \mathcal{A}_\text{demi-disques}$$ Si on note $a$ la longueur d'un des côtés du carré alors $$\mathcal{A}_\text{demi-disques} = 4 \times \frac12 \times \pi \left(\frac{a}{2}\right)^2 = \frac{\pi a^2}{2}$$

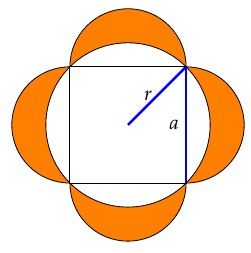
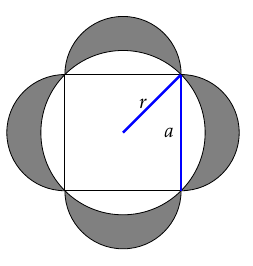
- Deuxième façon, sur la figure de droite. L'aire totale $\mathcal{A}$ se décompose cette fois en l'aire $\mathcal{A}_\text{disque}$ du disque (zone vert clair) et l'aire $\mathcal{A}_\text{lunules}$ formée par $4$ lunules (zone vert foncé, dont on veut aussi calculer l'aire) : $$\mathcal{A} = \mathcal{A}_\text{disque} + \mathcal{A}_\text{lunules}$$ Le rayon du cercle est $r = \frac{\sqrt{2}}{2}a$. Ainsi $$\mathcal{A}_\text{disque} = \pi r^2 = \pi \left(\frac{\sqrt{2}}{2}a\right)^2 = \frac{\pi a^2}{2}$$

- Conséquence $\mathcal{A}_\text{demi-disques} = \mathcal{A}_\text{disque}$ donc $$\mathcal{A}_\text{lunules} = \mathcal{A} - \mathcal{A}_\text{disque} = \mathcal{A} - \mathcal{A}_\text{demi-disques} = \mathcal{A}_\text{carré}$$
L'aire des lunules égale l'aire du carré !












