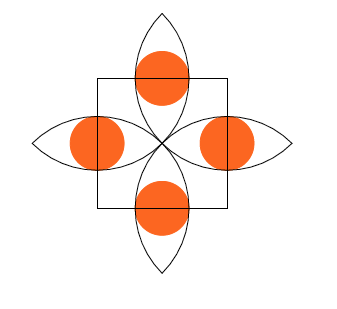
Enoncé du problème n° 19
- Sur la figure, le côté du carré a pour longueur 2, les quatre demi-cercles ont leurs centres aux sommets du carré et passent tous par le centre du carré.
- Les disques en orange ont leurs centres sur les côtés du carré et sont tangents aux demi-cercles.
- Quelle est l'aire totale coloriée ?
Auteur : Luc GIRAUD
Correction du problème n° 19
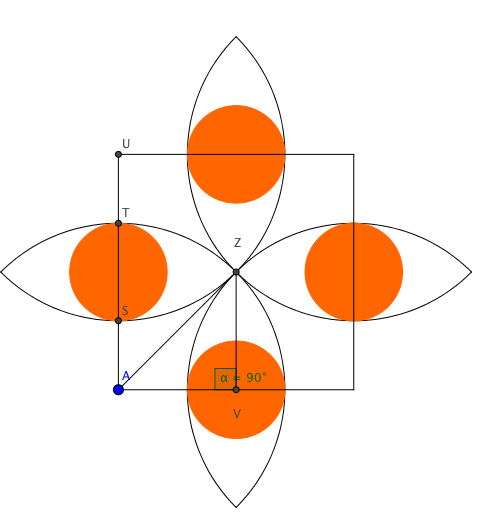
- En appliquant le théorème de Pythagore, dans le triangle $AVZ$ rectangle en $V$ :
$AV^2+VZ^2= AZ^2$
d'où $AZ^2=2$, soit $AZ=\sqrt 2$. - On note $D$ le diamètre d'un des petits disques oranges.
On a ( figure ci-dessous ), comme le côté du carré est 2 : $$\begin{array}{rlc} AS+ST+TU = 2&\iff 2\ell +D= 2 & \text{ où } \ell = AS= TU \\ &\iff D= 2(1-\ell)&\\ \end{array} $$ Par ailleurs : $$\begin{array}{rlc} AT+TU = 2&\iff \sqrt 2 +\ell = 2 & \text{ car }AT =AZ=\sqrt 2 \\ &\iff \ell = 2 - \sqrt 2 &\\ \end{array} $$ On a donc : $$\begin{array}{rl} D&=2(1-\ell) \\ & = 2\left( 1-2+\sqrt 2\right) \\ &= 2 \left( \sqrt 2 -1\right) \\ \end{array} $$ Leur rayon est donc $r=\sqrt 2-1$, on déduit alors l'aire des 4 disques oranges : $\mathcal{ A}= 4\pi r^2$ $$\begin{array}{rl} \mathcal{ A}= 4\pi r^2&= 4\pi \left( \sqrt 2 -1\right)^2 \\ & =4\pi\left( 2-2\sqrt 2+1\right) \\ &= 4\pi\left( 3-2\sqrt 2 \right) \\ &\approx 2,156 \textbf{ cm} ^2 \end{array} $$
Conclusion : L'aire totale des 4 disques est $\mathcal{ A}= 4\left (3-2\sqrt 2\right )\pi\approx 2,156$ cm $^2$ .













