Enoncé du problème n° 21
- Le gardien d’un phare s’est absenté en laissant la porte ouverte.
- Mais il ne craint pas les intrus : son chien de garde, féroce, veille au grain.
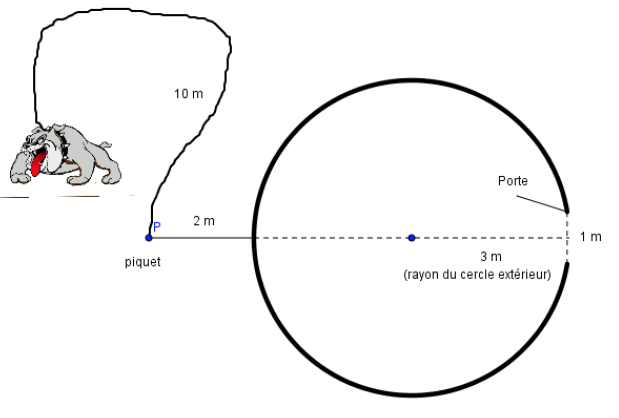
- Il est attaché par une chaine de 10 m à un piquet planté à 2 m du phare, diamétralement opposé à la porte. Celle-ci a une largeur de 1 m.
- Le rayon du phare (cercle extérieur) est de 3 m. La figure ci-dessous résume la situation.
- Malgré la présence du chien, quelqu’un peut-il tout de même s’introduire dans le phare ?
Auteur : Lionel DARIE
Correction du problème n° 21
- Il s’agit de déterminer si le chien peut atteindre la porte, en tendant au maximum sa chaine.
La situation est traduite par le schéma suivant :
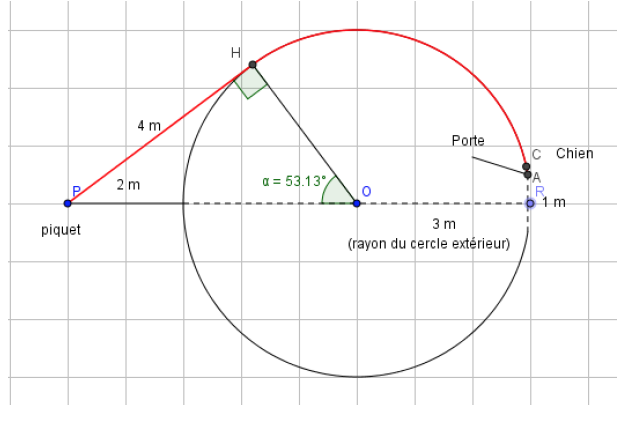
- Le chien, en tirant sur sa chaine, va d’abord « tangenter » le bord du phare en $H$. $O$ étant le centre du phare et $P$ le piquet, le triangle $OPH$ est rectangle en $H$. On applique le théorème de Pythagore : $$OP^2 = OH^2 + PH^2$$ donc : $$PH^2 = OP^2 - OH^2$$ Soit : $$PH^2 = (3 + 2)^2 - 3^2 = 16.$$ Donc $PH = 4$ m.
- Ensuite, le chien va enrouler les 6 m de chaine qui lui reste autour du phare.
Le point $A$ représente le bord de la porte et $R$ le milieu de l’ouverture de la porte.
Appelons $\alpha$ l’angle $\hat{POH}$. On a $\cos \alpha = \dfrac{3}{5}$
donc $\alpha \approx 53,13°$.
Ainsi, l’angle $\hat{ROH }= 180 – 53,13 = 126,87°$.
La longueur de l’arc $HR$ est : $$3 \times 126,87\times \dfrac{\pi}{180} \approx6,64 \text{m}.$$ On considère que l’arc $AR$ et la longueur du segment $[AR]$ sont quasiment égaux, à 0,5 m,
donc l’arc $HA$ mesure environ $6,64 – 0,5 = 6,14$ m.
Comme, à partir de $H$, il restait 6 m de chaine, cela signifie que le chien n’atteindra pas tout-à-fait le bord de la porte.
Conclusion : Il sera donc possible de se glisser à l’intérieur du phare !












