Enoncé du problème n° 23
- Vous aimez les équations, vous adorez la trigonométrie, en particulier les sinus et les cosinus! cette énigme est pour vous!
- Résoudre dans $\mathbb R$ : $$\sqrt{\cos(x)} + \sqrt{\sin(x)} = 1$$
Auteur : Luc GIRAUD

Correction du problème n° 23
- Méthode 1: On étudie $f: x\mapsto \sqrt{\cos(x)} + \sqrt{\sin(x)}$

- Il est clair que $f$ est périodique de période $2\pi$ car les fonctions $\sin$ et $\cos$ le sont.
Par ailleurs sur $[0;2\pi]$; $f(x)$ existe ssi $\left\lbrace \begin{array}{l} \cos x \geqslant 0\\ \sin x \geqslant 0 \end{array} \right. $ soit $x\in \left[0; \dfrac{\pi}{2}\right].$
$f$ est dérivable partout où les fonctions $\cos$ et $\sin$ sont dérivables et strictement positives , donc sur $[0;2\pi]$, $f$ est dérivable sur $\left]0; \dfrac{\pi}{2}\right[ .$
Comme $\left( \sqrt u\right) '= \dfrac{u'}{2\sqrt u}$; on trouve : $$f'(x)= -\dfrac{\sin x}{2\sqrt {\cos x}}+\dfrac{\cos x }{2\sqrt {\sin x}}= \dfrac{\sqrt{\cos x }^3-\sqrt{\sin x }^3}{2\sqrt {\sin x\cos x}}$$ A partir du cerlce trigonométrique, on lit facilement sur $\left]0; \dfrac{\pi}{4}\right[ .$ : $$\begin{array}{cl} \cos x >\sin x & \\ \sqrt{\cos x } > \sqrt{\sin x } & \text{ car la fonction } x\mapsto \sqrt x \text{ est strictement croissante sur } \mathbb R ^+ \\ \sqrt{\cos x }^3> \sqrt{\sin x }^3 & \text{ car la fonction } x\mapsto x^3 \text{est strictement croissante sur } \mathbb R\\ \sqrt{\cos x }^3 - \sqrt{\sin x }^3 > 0&\\ \dfrac{\sqrt{\cos x }^3-\sqrt{\sin x }^3}{2\sqrt {\sin x\cos x}}> 0 &\text{ car } 2\sqrt {\sin x\cos x}> 0 \text{ sur } \left]0; \dfrac{\pi}{4}\right[\\ f'(x)> 0& \end{array}$$ On prouve de même $f'(x)< 0$ sur $\left] \dfrac{\pi}{4}; \dfrac{\pi}{2}\right[ .$ On déduit le tableau de variations de $f $ sur $\left[0; \dfrac{\pi}{2}\right]$:Il apparaît alors clairement : $$\mathcal{S}_{\left[0; \dfrac{\pi}{2}\right]}=\{0; \dfrac{\pi}{2} \}$$ Puis $\mathcal{S}=\{\dfrac{\pi}{2}+k2\pi; k2\pi /k\in \mathbb Z\}$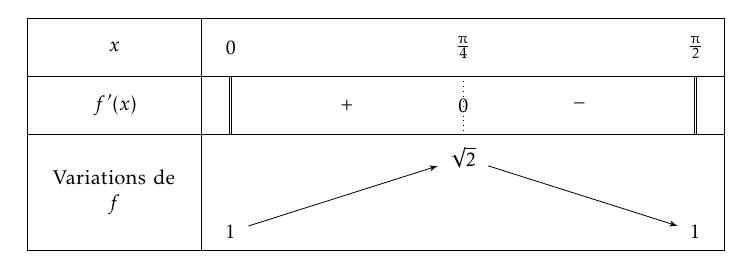
- Méthode 2: On sait que si $a\in]0;1[$ alors $a^2 < a < \sqrt{a}$
On déduit donc : $$\sqrt{\cos(x)} + \sqrt{\sin(x)} > \cos(x)^2+\sin(x)^2$$ Mais on sait que pour tout réel $x$, on a : $$\cos(x)^2+\sin(x)^2= 1$$ - On déduit donc si $\cos x \in ]0;1[$ et si $\sin x \in ]0;1[$ alors $f(x)> 1$
Ce qui prouve que si $f(x)=1$, alors nécessairement $\cos x =0$ ou $\cos x =1$ ... -
Conclusion: $\mathcal{S}=\{\dfrac{\pi}{2}+k2\pi; k2\pi /k\in \mathbb Z\}$












