• Un chimiste réalise un drôle de cocktail : dans un verre conique, il verse successivement du mercure (densité 13,59), de l’eau (densité 1) et de l’huile (densité 0,915).
  Les trois liquides remplissent le verre sans se mélanger en y formant trois couches d’égale épaisseur.
  Le verre contient-t-il alors une masse plus importante d’eau, d’huile ou de mercure ? Rappel : Masse = densité $\times$ volume.

Auteur : Lionel DARIE

• La situation correspond à la figure suivante :
  

  

  Chaque couche (huile, eau, mercure) a la même épaisseur $h$.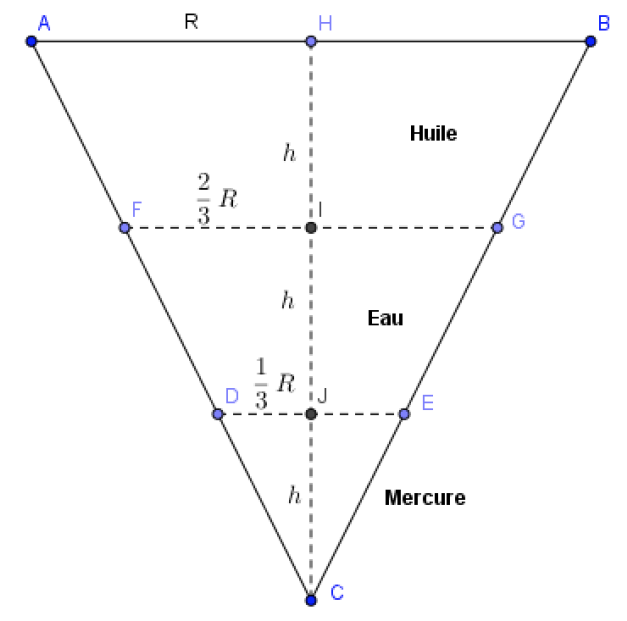
  Le rayon de la base du cône est $AH = R$.
  A l’aide du théorème de Thalès, on calcule les rayons des cercles délimitant respectivement les couches d’huile et d’eau ( $FI = \dfrac{2}{3 }R$) et les couches d’eau et de mercure ($DJ = \dfrac{1}{3 }R$ ) :
  Les triangles $AHC$ et $FIC$ sont en situation de Thalès donc :
  $\dfrac{FI}{AH} = \dfrac{IC}{HC}$ soit : $\dfrac{FI}{R} =\dfrac{h}{ 3h}$ d’où : $FI = \dfrac{2}{3} R$.
  De même, les triangles $AHC$ et $DJC$ sont en situation de Thalès donc :
  $DJAH = JCHC$ soit : $\dfrac{DJ}{R} = \dfrac{h}{3 h}$ d’où : $DJ = \dfrac{1}{3} R$.
  Volume du mercure : le volume d’un cône est $V = \dfrac{1}{3} \times \text{Base}\times \text{ hauteur}$.
  Ici la base est un disque de rayon $DJ = \dfrac{1}{3} R$ la hauteur est $h$. Donc :
  $V_m = \dfrac{1}{3} \pi \times \left( \dfrac{1}{3} R\right)^2 \times h = \dfrac{1}{27}\pi h R^2$
  Masse du mercure : $M_m = 13,59 \times V_m = 13,59 \times \dfrac{1}{27}\pi h R^2 = 0,503 \pi h R ^2$.
  Volume de l’eau : C’est la différence des volumes de deux cônes : $V_e = \dfrac{1}{3} \pi \times \left( \dfrac{2}{3} R\right)^2 \times 2 h-\dfrac{1}{27}\pi h R^2$
  Soit :$V_e =\dfrac{8}{27} h\pi R ^2 –\dfrac{1}{27}\pi h R^2$
  D’où $Ve = \dfrac{7}{27}\pi h R^2$ Masse de l’eau : $M_e = 1 \times V_e = \dfrac{7}{27}\pi h R^2 \approx 0,259 \pi h R ^2$.
  Volume de l’huile : on procède encore par différence :
  $V_h = \dfrac{1}{3} \pi h R^2 \times 3 h – \dfrac{8}{27} h\pi R ^2$
  Soit : $V_h = \pi h R^2 h – \dfrac{8}{27} h\pi R ^2$
  D’où : $V_h = \dfrac{19}{27}\pi h R^2$
  Masse de l’huile : $M_h = 0,915\times V_h = 0,915 \dfrac{19}{27}\pi h R^2 \approx 0,644 \times \pi h R ^2$.