Enoncé du problème n° 32
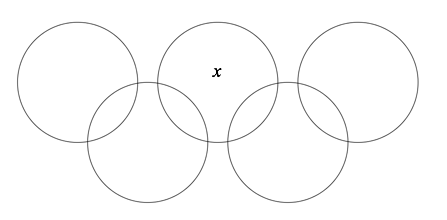
- Ces cinq cercles délimitent 9 zones dans lesquelles on inscrit les chiffres de 1 à 9, de telle sorte que la somme des chiffres de chaque disque soit égale à 11.
- Quelle est la valeur de \(x\) ?
Auteur : Delphine GUILLERMARD
Correction du problème n° 32
Voici les différentes possibilités pour écrire 11 comme la somme de deux chiffres distincts, ou bien de trois chiffres distincts : $$\begin{array}{rl} 11 &= 9 + 2 \\ 11 &= 8 + 3 \\ 11 &= 7 + 4 \\ 11 &= 6 + 5 \\ 11 &= 1 + 2 + 8 \\ 11 &= 1 + 3 + 7 \\ 11 &= 1 + 4 + 6 \\ 11 &= 2 + 3 + 6 \\ 11 &= 2 + 4 + 5 \\ \end{array}$$ Les sommes de deux termes donnent les différentes possibilités pour les nombres a et b d’une part, et g et h d’autre part.
On remarque que le chiffre 9 n’apparaît pas dans les sommes de trois chiffres, donc a ou h est forcément 9.
La figure étant symétrique, choisissons \( a = 9\). Ce qui donne immédiatement \( b = 2\).
On remarque maintenant que les chiffres 5 et 7 apparaissent dans une seule des sommes de trois chiffres, donc ce sont les nombres \( c\) et \( f \).
Si \( c = 7\), alors, comme \( b + c + d = 11\), avec \( b = 2\), on aurait \( d = 2\), ce qui n’est pas possible car le chiffre 2 est déjà inscrit. On en déduit que \( f = 7\) et \( c = 5\).
Revenons aux écritures de 11 comme somme de deux chiffres : les chiffres 9, 2, 5 et 7 étant déjà inscrits sur la figure, il en résulte que \( g + h = 3 + 8\). Comme \( f = 7\), on ne peut pas avoir \( g = 8\) (car la somme des chiffres du disque en bas à droite dépasserait 11), donc \( g = 3\) et \( h = 8\).
- Ces cinq cercles délimitent 9 zones dans lesquelles on inscrit les chiffres de 1 à 9, de telle sorte que la somme des chiffres de chaque disque soit égale à 11.
- Quelle est la valeur de \(x\) ?
Auteur : Delphine GUILLERMARD
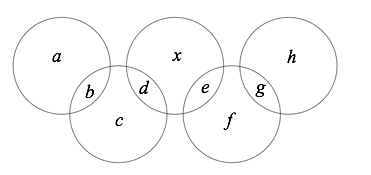
Voici les différentes possibilités pour écrire 11 comme la somme de deux chiffres distincts, ou bien de trois chiffres distincts : $$\begin{array}{rl} 11 &= 9 + 2 \\ 11 &= 8 + 3 \\ 11 &= 7 + 4 \\ 11 &= 6 + 5 \\ 11 &= 1 + 2 + 8 \\ 11 &= 1 + 3 + 7 \\ 11 &= 1 + 4 + 6 \\ 11 &= 2 + 3 + 6 \\ 11 &= 2 + 4 + 5 \\ \end{array}$$ Les sommes de deux termes donnent les différentes possibilités pour les nombres a et b d’une part, et g et h d’autre part.
On remarque que le chiffre 9 n’apparaît pas dans les sommes de trois chiffres, donc a ou h est forcément 9.
La figure étant symétrique, choisissons \( a = 9\). Ce qui donne immédiatement \( b = 2\).
On remarque maintenant que les chiffres 5 et 7 apparaissent dans une seule des sommes de trois chiffres, donc ce sont les nombres \( c\) et \( f \).
Si \( c = 7\), alors, comme \( b + c + d = 11\), avec \( b = 2\), on aurait \( d = 2\), ce qui n’est pas possible car le chiffre 2 est déjà inscrit. On en déduit que \( f = 7\) et \( c = 5\).
Revenons aux écritures de 11 comme somme de deux chiffres : les chiffres 9, 2, 5 et 7 étant déjà inscrits sur la figure, il en résulte que \( g + h = 3 + 8\). Comme \( f = 7\), on ne peut pas avoir \( g = 8\) (car la somme des chiffres du disque en bas à droite dépasserait 11), donc \( g = 3\) et \( h = 8\).
Conclusion : Les derniers chiffres se déduisent facilement, et on obtient ainsi : \(x = 6\).












