Un étudiant se rend tous les jours à la fac en vélo. Il fait le trajet à 20 km/h de moyenne. À quelle vitesse doit-il aller au retour pour que sa vitesse moyenne sur l’aller-retour soit de 40 km/h?
Illustrons le problème :
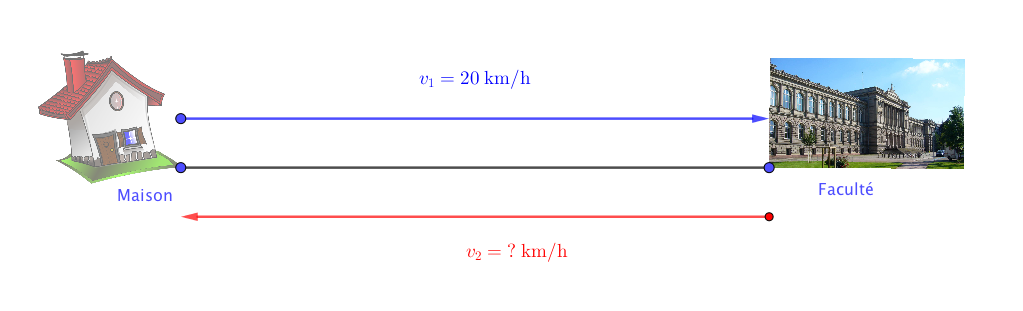
Si on nomme :
- \(d\) la distance séparant la maison de la faculté,
- \(v_1\) la vitesse durant le trajet Maison \(\rightarrow\) Faculté
- \(t_1\) le temps pour faire le trajet Maison \(\rightarrow\) Faculté
- \(v_2\) la vitesse durant le trajet Faculté\(\rightarrow\) Maison
- \(t_2\) le temps pour faire le trajet Faculté\(\rightarrow\) Maison
- \(v_{\text{Moyen}}\) la vitesse moyenne durant le trajet Maison \(\rightarrow\)Faculté\(\rightarrow\) Maison
On a \(v_1 =20\)
On veut que \(v_{\text{Moyen}}=40\)
On a \(v_1=\dfrac{d}{t_1}\) , \(v_2=\dfrac{d}{t_2}\) et \(v_{\text{Moyen}}=\dfrac{2d}{t_1+t_2}\)
Comme \(v_1=\dfrac{d}{t_1}\), on déduit \(t_1=\dfrac{d}{v_1}\) ; de même \(t_2=\dfrac{d}{v_2}\)
$$v_{\text{Moyen}}=\dfrac{2d}{t_1+t_2}= \dfrac{2d}{\dfrac{d}{v_1}+\dfrac{d}{v_2}}= \dfrac{2}{\dfrac{1}{v_1}+\dfrac{1}{v_2}}$$
On déduit donc $$\dfrac{v_{\text{Moyen}}}{2}= \dfrac{1}{\dfrac{1}{v_1}+\dfrac{1}{v_2}}$$
Soit en prenant les inverses :
$$\dfrac{2}{v_{\text{Moyen}}}= \dfrac{1}{v_1}+\dfrac{1}{v_2}$$
Si on reprend les données du problème, on obtient :
$$\dfrac{2}{40}= \dfrac{1}{20}+\dfrac{1}{v_2} \iff \dfrac{1}{v_2}= 0$$
Ce qui n'est pas possible !












