Un problème classique, autrefois dans les écoles militaires, constituait à déterminer le nombre de boulets que l'on entassait à proximité des canons.Les entassements pratiqués étaient sous forme de pyramide à base carrée ou à base triangulaire.

• Déterminer en fonction de $k$ le nombre de boulets d'une couche.

  

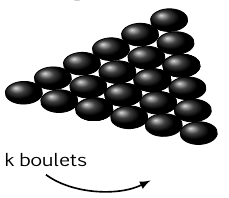
• Montrer que le nombre de boulets à $n$ couches est $\dfrac{n(n+1)(n+2)}{6}$.
• Montrer qu'avec les boulets d'une pyramide à 8 couches et ceux d'une pyramide à 14 couches il est possible de constituer une autre pyramide. ( préciser le nombre de couches) .

Auteur : Luc GIRAUD

• Le nombre de boulets de la couche n° $k$ est $T_k=1+2+3+\cdots k$
  En utilisant la relation donnant la somme des termes successifs d'une suite arithmétique de raison 1, il vient : $$\begin{array}{rl} T_k&= \dfrac{ N\times (P+D)}{2} \\ & = \dfrac{ k (k+1)}{2} \\ \end{array}$$ Le nombre de boulets d'une pyramide à $n$ couches est donc $$\begin{array}{rl} S_n& = T_1+T_2+T_3+\cdots + T_n\\ &= \dfrac{ 1\times 2}{2} +\dfrac{ 2\times 3}{2}+\dfrac{ 3\times 4}{2}+\cdots+\dfrac{ n\times (n+1) }{2}\\ \end{array}$$ Prouvons donc la propriété $\mathcal{P}_n :S_n= \dfrac{ 1\times 2}{2} +\dfrac{ 2\times 3}{2}+\dfrac{ 3\times 4}{2}+\cdots+\dfrac{ n\times (n+1) }{2}= \dfrac{ n\times (n+1)(n+2) }{6} $, à l'aide d'un raisonnement par récurrence.
  • Initialisation :$S_1= \dfrac{ 1\times 2}{2}= 1$ et $ \dfrac{ 1\times 2\times 3 }{6}=1$ donc $\mathcal{P}_1$ est vraie.
  • Hérédité : soit $k\geqslant 1$, on suppose que $\mathcal{P}_k$ est vraie; on a donc par hypothèse : $$ S_k= \dfrac{ 1\times 2}{2} +\dfrac{ 2\times 3}{2}+\dfrac{ 3\times 4}{2}+\cdots+\dfrac{ k\times (k+1) }{2}= \dfrac{ k\times (k+1)(k+2) }{6} $$ Calculons $S_{k+1}$: $$\begin{array}{rl} S_{k+1}&= S_k+ T_{k+1} \\ & =\dfrac{ k\times (k+1)(k+2) }{6}+ \dfrac{ (k+1)\times (k+2) }{2}\\ &=\dfrac{ k\times (k+1)(k+2) }{6}+ \dfrac{ 3(k+1)\times (k+2) }{6}\\ &=\dfrac{ k\times (k+1)(k+2) +3(k+1)\times (k+2)}{6}\\ &= \dfrac{ (k+1)(k+2)(k+3)}{6} \end{array}$$ Ce qui montre que si $\mathcal{P}_k$ est vraie alors $\mathcal{P}_{k+1} $ est vraie. Ainsi la propriété $\mathcal{P}_n$ est héréditaire à partir du rang 1.
  • Conclusion : $\mathcal{P}_1$ est vraie, et $\mathcal{P}_n$ est héréditaire à partir du rang 1.
    Le principe de récurrence s'applique et donc pour tout entier $n \geqslant 1$, $\mathcal{P}_n$ est vraie.
  Une pyramide à 8 couches contient $S_8$ boulets, or $S_8= \dfrac{8\times 9\times 10 }{6}=\dfrac{720 }{6}$
  et une pyramide à 14 couches contient $S_{14}$ boulets, or $S_{14}= \dfrac{14\times 15\times 16 }{6}=\dfrac{3360 }{6}$
  On remarque alors que $S_8+S_{14}=\dfrac{720 }{6}+\dfrac{3360 }{6}=\dfrac{4080 }{6}=\dfrac{15\times 16\times 17}{6}=S_{15}$