• En hiver, un enfant lance un ballon dans un étang. Le ballon flotte et s’éloigne de la rive.
• Dans la nuit, l’eau de l’étang gèle et le ballon se retrouve partiellement pris dans la glace.
• Le lendemain, l’enfant s’aventure alors sur la surface gelée de l’étang et, sans casser la glace, réussit à récupérer le ballon.
• Celui-ci a laissé un trou de 24 cm de diamètre et de 8 cm de profondeur.
• Saurez – vous retrouver le rayon du ballon, en centimètres ?

Auteur : Lionel DARIE

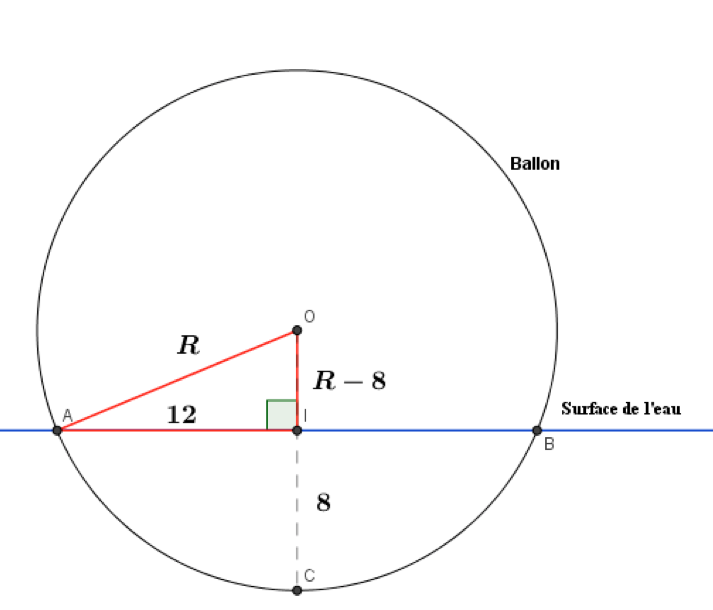
• La situation correspond à la figure ci-dessous. $AB = 24$ est le diamètre du trou laissé dans la glace.

• $I$ est le milieu de $[AB]$, c’est le centre du cercle, bord du trou dans la glace. $IC = 8$ est la profondeur du trou.
• $R$ est le rayon du ballon. $OC = R$ donc $OI = R – 8$.
• Dans le triangle $OAI$, rectangle en $I$, on applique le théorème de Pythagore : $OA^2 = OI^2 + AI^2$
• Donc : $R^2 = (R – 8)^2+ 12^2$ On obtient ainsi une équation d’inconnue le rayon $R$, que l’on va résoudre en développant d’abord le carré $(R – 8)^2$.
• Donc, successivement : $R^2 = R^2 – 16 R + 64 + 144$
• $0 = – 16 R + 208$ (en retranchant $R^2$ dans chaque membre) $16 R = 208$
• $R = = 13$.
  Conclusion : le rayon du ballon est $R = 13 cm$.