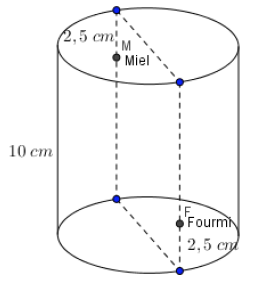
• On place une goutte de miel à l’intérieur d’un verre cylindrique, à 2,5 cm du bord.
• Une fourmi se trouve aussi sur le verre, en face de la goutte de miel, mais sur la paroi extérieure, à 2,5 cm du fond.
• La hauteur du verre est de 10 cm et la circonférence de base est de 25 cm.
• Quel chemin doit suivre la fourmi sur les parois du verre pour atteindre le miel en parcourant le minimum de distance possible ? Quelle est cette distance minimale ?

Auteur : Lionel DARIE

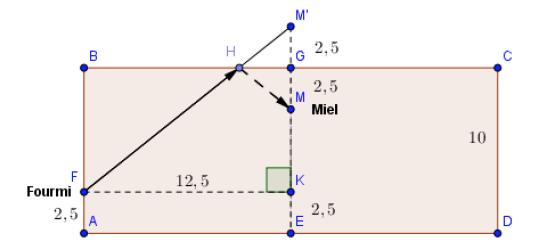
• On réalise un patron de la surface latérale du cylindre. Imaginer un rectangle de longueur 25 cm et de largeur 10 cm, que l’on enroule autour du verre. Le côté gauche et le côté droit de ce rectangle vont se raccorder exactement le long de la verticale où se trouve la fourmi au départ. Si on « étale » à plat se patron, on obtient la figure suivante :

• Pour que la fourmi atteigne la goutte de miel, elle doit d’abord se déplacer jusqu’au bord du verre, ceci sur la paroi extérieure (trajet de $F$ vers $H$), puis basculer à l’intérieur du verre et effectuer le trajet de $H$ à $M$. Le problème est de trouver la position du point H pour que le trajet total soit le plus petit possible. On considère le point $M’$, symétrique de $M$ par rapport à la droite $(BC)$ (voir figure). $(BC)$ est donc la médiatrice de $[MM’]$. Soit $d $ la distance parcourue par la fourmi pour atteindre le miel (point $M$).
• On a : $$d = FH + HM$$ Or, $HM = HM’$, puisque $(BC)$ est la médiatrice de $[MM’]$. Donc : $d = FH + HM’$.
• Le plus court chemin pour aller du point $F$ au point $M’$ est la ligne droite.
  Ainsi, la distance $d $ sera minimale si les points $F , H$ et $M’$ sont alignés.
  Pour placer le point $H$, il suffit donc de tracer le segment $[FM’]$. Celui-ci coupe la droite $(BC)$ en $H$.
  Pour obtenir le trajet réel de la fourmi, il suffit de replacer le patron autour du verre.
  Les segments $[FH]$ et $[HM]$ vont se « courber » et deviendront des morceaux d’hélice.

Calcul de la distance d minimale :

• On se place dans le triangle rectangle $FM’K$, rectangle en $K$ (voir figure)
  $$d = FM’$$ $$FK = 12,5$$ $$KM’ = 10$$
• Appliquons le théorème de Pythagore :
  $FM’^2 = FK^2 + KM’^2$ soit : $d^2=\left(\dfrac{25}{2}\right)^2+102=\dfrac{1025}{4}$ d’où $d=\sqrt{\dfrac{1025}{4}} =\dfrac{ 5}{2}\sqrt{41}$.