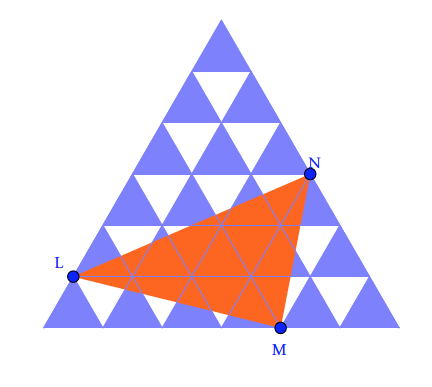
• Le grand triangle équilatéral est découpé en 36 petits triangles équilatéraux.
ayant tous la même aire 1.
• Quelle est l'aire du triangle LMN ?

Auteur : Luc GIRAUD

• Le grand triangle équilatéral est découpé en 36 petits triangles équilatéraux.
ayant tous la même aire 1.
• Quelle est l'aire du triangle LMN ?

Auteur : Luc GIRAUD

• En posant $a$ l'aire d'un petit triangle équilatéral, on a $a=\dfrac{2}{\sqrt{\sqrt 3} }$
$$LM^2= 13 a^2, MN^2=7a^2, LN^2= 19a^2$$
• L'aire de $LMN$ vaut $$S=\dfrac{1}{2} bc\sin \hat A $$ Et AlKashi donne $$\cos \hat A =\dfrac{b^2+c^2-a^2}{2bc}$$ $$S^2=\dfrac{1}{4} b^2c^2\sin ^2\hat A $$ $$S^2=\dfrac{1}{4} b^2c^2\left (1-\cos ^2\hat A \right )$$ $$S^2=\dfrac{1}{4} b^2c^2\left (1-\left(\dfrac{b^2+c^2-a^2}{2bc}\right )^2 \right )$$ $$S^2=\dfrac{1}{16} \left( 4b^2c^2-\left (b^2+c^2-a^2\right )^2\right ) $$ AN: on trouve $$S=11$$