Enoncé du problème n° 27
- « Si je multiplie ensemble quatre entiers consécutifs et que j'ajoute un, je trouve un carré parfait. »
- C'est vrai ou c'est faux ?
- Cette conjecture est-elle vraie ?
Auteur : Luc GIRAUD

Correction du problème n° 27
-
Avec un tableur, on obtient sans peine :
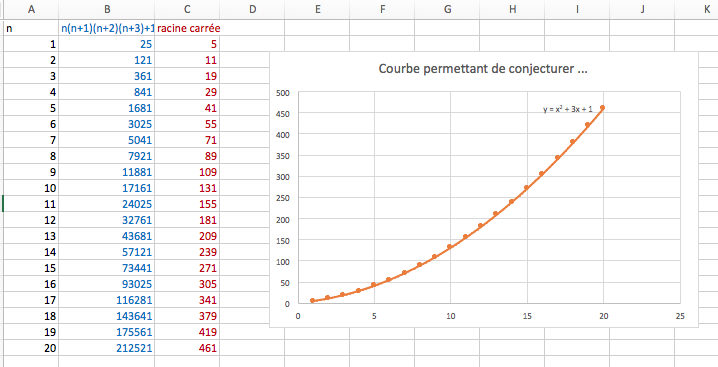
- $$\begin{array}{rl} n(n+1)(n+2)(n+3)+1& =(n^2+n)(n^2+5n+6)+1\\ & =n^4+5n^3+6n^2+n^3+5n^2+6n+1\\ &=n^4+6n^3+11n^2+6n+1\\ &\\ (n^2+3n+1)^2&=n^4+9n^2+1+6n^3+2n^2+6n\\ &=n^4+6n^3+11n^2+6n+1\\ \end{array}$$
Conclusion : pour tout entier naturel $n$: $n(n+1)(n+2)(n+3)+1=(n^2+3n+1)^2$












