• Un seigneur a décidé d'installer des péages à tous les croisements de routes.
  Evidemment il a oublié d'en préciser les tarifs.
  Voici tout ce que l'on sait :
  En voyageant vers l'est, on trouve successivement un péage de 7 sous puis un péage de 13 sous.
  Les tarifs additionnés des 3 péages les plus au nord valent 22 sous, le péage central étant aussi cher à lui seul que les deux autres réunis.
  Les tarifs additionnés des 3 péages les plus au sud valent 31 sous, le péage central coûtant 3 sous de moins que les deux autres réunis.
  Un voyageur qui traverse le centre du pays du nord au sud ou d'est en ouest, paie, dans les deux cas, 32 sous.
  Le péage le moins cher vaut 5 sous, il n'est ni au sud, ni à l'ouest.
  Le péage le plus cher vaut 14 sous.
  Le péage le moins cher des péages du sud est à l'ouest.
  Tous les prix des péages sont différents.
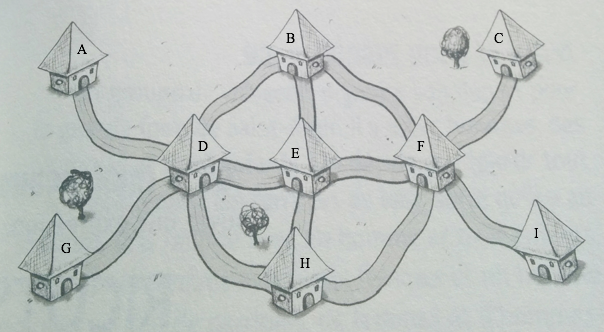
  Voici un plan de la région. Les petites maisons sont les péages installés par le seigneur.

Auteur : Florence TOURNIER

• La situation correspond à la figure suivante :
  

  

  Les tarifs additionnés des 3 péages les plus au nord valent 22 sous, le péage central étant aussi cher à lui seul que les deux autres réunis.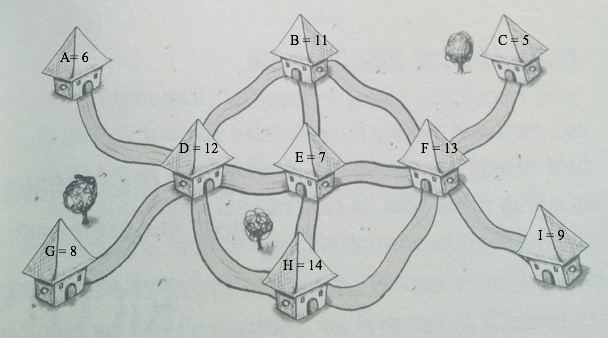
  Donc $A + B + C = 22$ et $ B = A + C $ donc $2B = 22 \iff B = 11$ et donc $A + C = 11.$
  Les tarifs additionnés des 3 péages les plus au sud valent 31 sous, le péage central coûtant 3 sous de moins que les deux autres réunis.
  Donc $G + H + I = 31$ et $H = G + I – 3$ $G + I = H + 3 $
  donc $2H + 3 = 31\iff H = 14$ donc $H = 14$ ( le péage le plus cher ) et $ G + I = 17$
  Un voyageur qui traverse le centre du pays du nord au sud ou d'est en ouest, paie, dans les deux cas, 32 sous.
  Donc $B + E + H = 32$ donc $E = 32 – 11 – 14$ d'où $E = 7$ et $ D + E + F = 32$ donc $ D + F = 32 – 7$ d'où $D + F = 25$
  En voyageant vers l'est, on trouve successivement un péage de 7 sous puis un péage de 13 sous.
  Le péage valant 7 sous est $E$. En voyageant vers l'est on rencontre ensuite $F$ donc $F = 13$.
  Or $D + F = 25$ donc $D = 25 – 13 $ d'où $D = 12$.
  Il nous reste donc $A + C = 11 $ et $ G + I = 17$.
  Le péage le moins cher vaut 5 sous, il n'est ni au sud, ni à l'ouest.
  $G$ et $I$ sont au sud , $A$ est à l'ouest . On en déduit donc que le péage le moins cher est $C$.
  Donc $C = 5$ . Par conséquent $A = 11 – 5$ donc $A = 6$.
  Le péage le moins cher des péages du sud est à l'ouest et tous les prix des péages sont différents.
  $G + I = 17$ .
  La seule possibilité restante avec des nombres compris entre 5 et 14 et non encore choisis est 9 + 8.
  $G$ est à l'ouest donc $G = 8$ et $I = 9$.