Il était d’usage dans le japon antique d’offrir aux dieux amateurs de Mathématiques des problèmes de géométrie gravés sur des tablettes.
C’était l’art du "sangaku".
Sur l’une des tablettes retrouvées, quelques coups de pinceau retraçaient l’énigme :

• le triangle est rectangle ;
 
• ses deux côtés de l’angle droit mesurent respectivement 8 et 15.

- Rayon du cercle circonscrit
En appliquant le théorème de Pythagore au triangle rectangle, on détermine que son hypoténuse mesure 17.
Le centre du cercle circonscrit d'un triangle rectangle est le milieu de son hypoténuse.
 On conclut donc que le rayon du grand cercle mesure \(\dfrac{15\times 8}{2}=60\)

- Rayon du cercle inscrit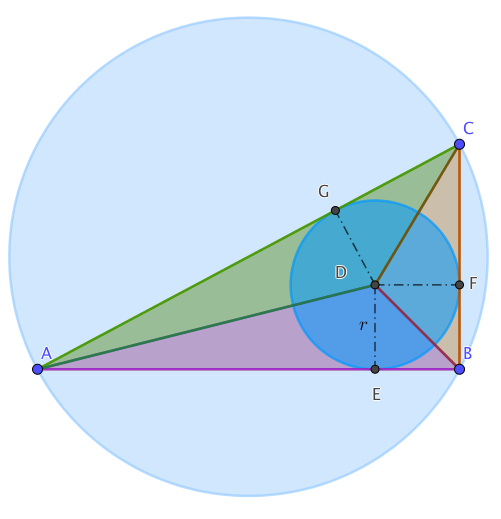

L'aire du triangle rectangle est égale à \(\dfrac{15\times 8}{2}=60\)
On peut découper le triangle rectangle en trois triangles ayant pour sommet commun le centre du cercle inscrit.
Si on appelle \(r\)le rayon du cercle inscrit, on peut exprimer en fonction de \(r\)  les aires des trois triangles formant le découpage : \(\dfrac{15r}{2}\),  \(\dfrac{8r}{2}\) et \(\dfrac{17r}{2}\).
En effet : $$\begin{array}{rlr} S_{\text{ABC}}& =S_{\text{DAB}}+S_{\text{DBC}}+S_{\text{DCA}}&\\ & =\frac{1}{2}AB\times DE+\frac{1}{2}BC\times DF +\frac{1}{2}CA\times DF &\\ &=\frac{r}{2}AB +\frac{r}{2}BC+\frac{r}{2}CA& \textbf{car } DE=DF=DG=r\\ &= \frac{15}{2}r+\frac{8}{2}r+\frac{17}{2}r \end{array}$$
On a ainsi l'équation : $$\dfrac{15r}{2}+\dfrac{8r}{2}+\dfrac{17r}{2}=60$$
 Après résolution de cette équation, on conclut donc que le rayon du petit cercle mesure \(3\).