Dans une classe de 30 élèves, quelle est la probabilité pour que 2 élèves fêtent leurs anniversaires le même jour?
Avec 365 jours par an, une trentaine d'élèves dans la classe, on se dit qu'elle doit être faible...
Eh bien justement, parlons en de la probabilité !
Il se trouve qu’elle n’est pas du tout négligeable :
dans un groupe d’environ 25 personnes, il y a plus de 50 % de chance que deux de ces personnes soient nées le même jour.
Ce résultat est tellement contraire à notre intuition qu’on l’appelle le paradoxe des anniversaires.
Pour les incrédules et les lycéens qui révisent les probabilités pour le bac, faisons ensemble le calcul pour un groupe de N personnes. Pour faire cela, on va prendre l'événement contraire, et calculer la probabilité P que toutes les personnes aient leur anniversaire un jour différent.
Et pour calculer cette probabilité, on va classiquement procéder par dénombrement.
Commençons par l’ensemble de tous les cas possibles :
pour la première personne, 365 dates sont possibles, pour la seconde aussi,
de même que pour la troisième
et toutes les autres.
Si on multiplie tout ça il y a donc 365\(^N \) cas possibles.
Maintenant quels sont les cas où les anniversaires sont tous différents :
pour la première personne il y a 365 choix,
pour la seconde il n’en reste que 364,
pour la troisième 363,
etc.
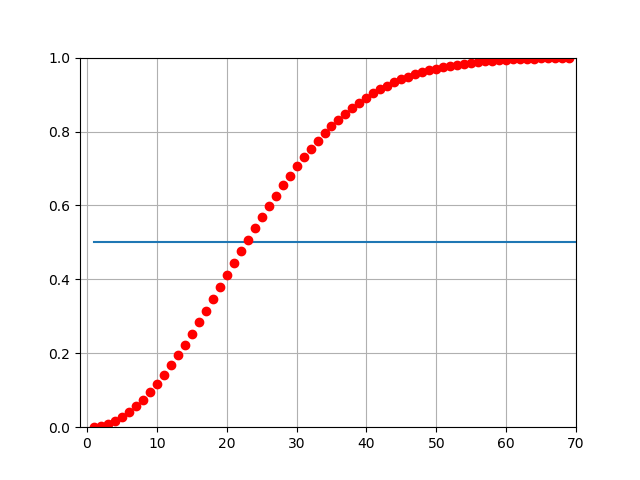
et pour la Nième seulement \((365-N+1)\). Si on multiplie tout ça on trouve la quantité \(365\times 36\times363\times\cdots (365-N+1)\) On peut donc calculer notre probabilité P qui vaut $$P= \dfrac{365\times 364\times363\times\cdots (365-N+1)}{365^N}$$ J’espère que vous me croyez pour l’application numérique, mais avec N=23 personnes on trouve P = 0,49.
Mais rappelez vous que P est la probabilité que les anniversaires soient tous différents.
Donc la probabilité qu’il y en ait au moins deux identiques est 1 - P, soit ici 0,51, c’est-à-dire 51 Et plus il y a de personnes dans le groupe, plus cette probabilité augmente.
Dans un groupe de 50 personnes, il y a plus de 95 % de chance que deux personnes aient leur anniversaire le même jour.
Une figure montrant l'évolution de cette probabilité :
# Probleme des anniversaires
def proba(n):
Card_univers=365**n
P=365
for j in range(1,n):
P=P*(365-j)
return 1-P/Card_univers
# Creation d'un nuage de points
from pylab import *
x=[]
y=[]
for i in range(1,70):
x.append(i)
y.append(proba(i))
import numpy as np
import matplotlib.pyplot as plt
z = np.array([1,70])
t = np.array([0.5, 0.5])
plt.plot(z, t)
plot(x, y, 'ro') # modif
plot([23],[proba(23)],'b')
axis([-1,70,0,1])
grid()
show()