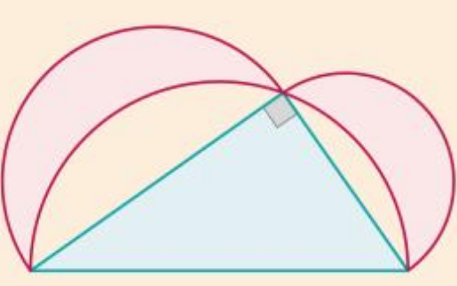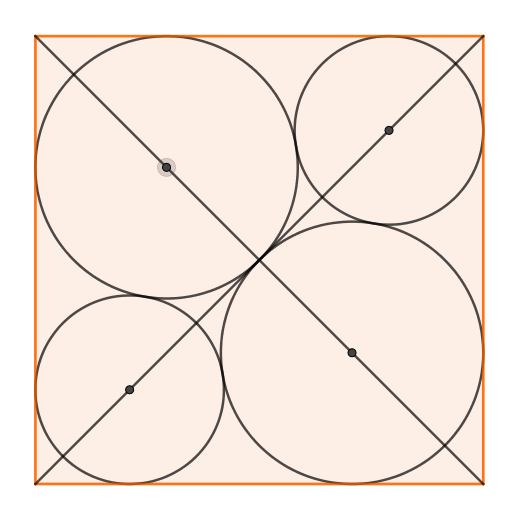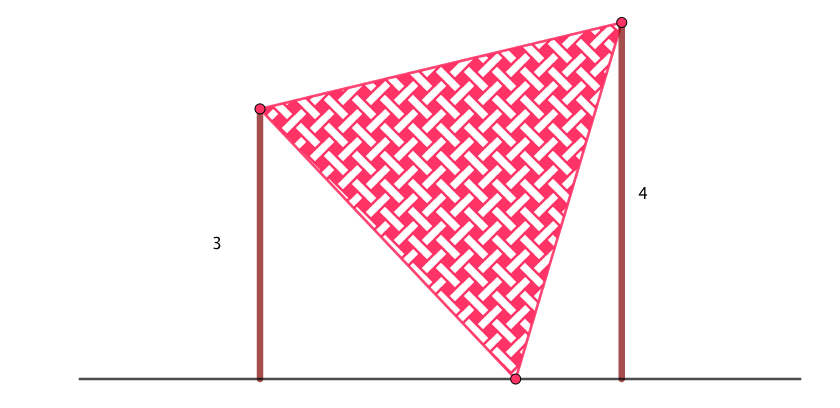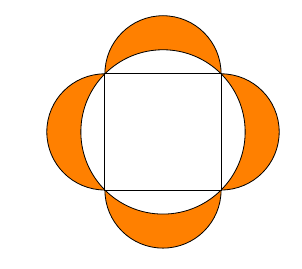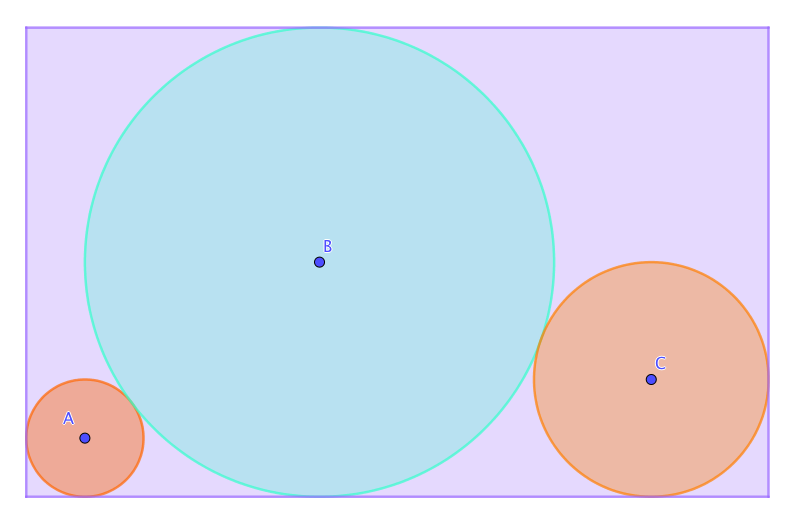
Déterminer la longueur du rectangle, lorsque les 3 cercles ont pour rayons respectifs 1, 4, 2.
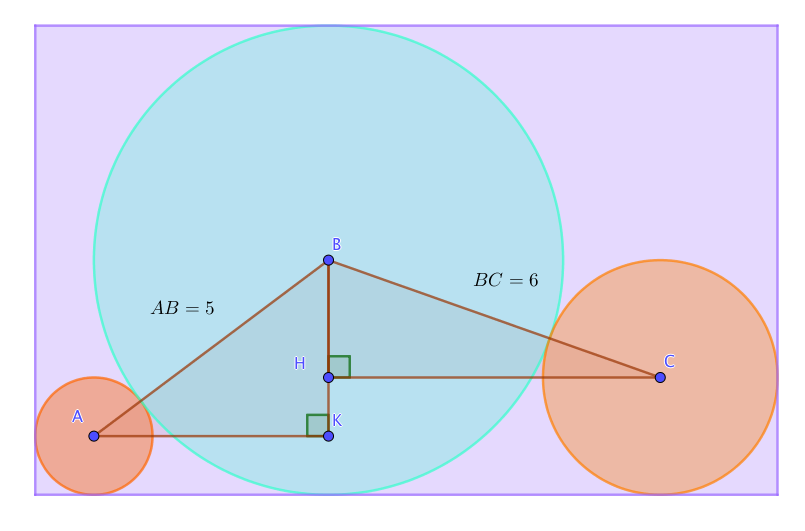
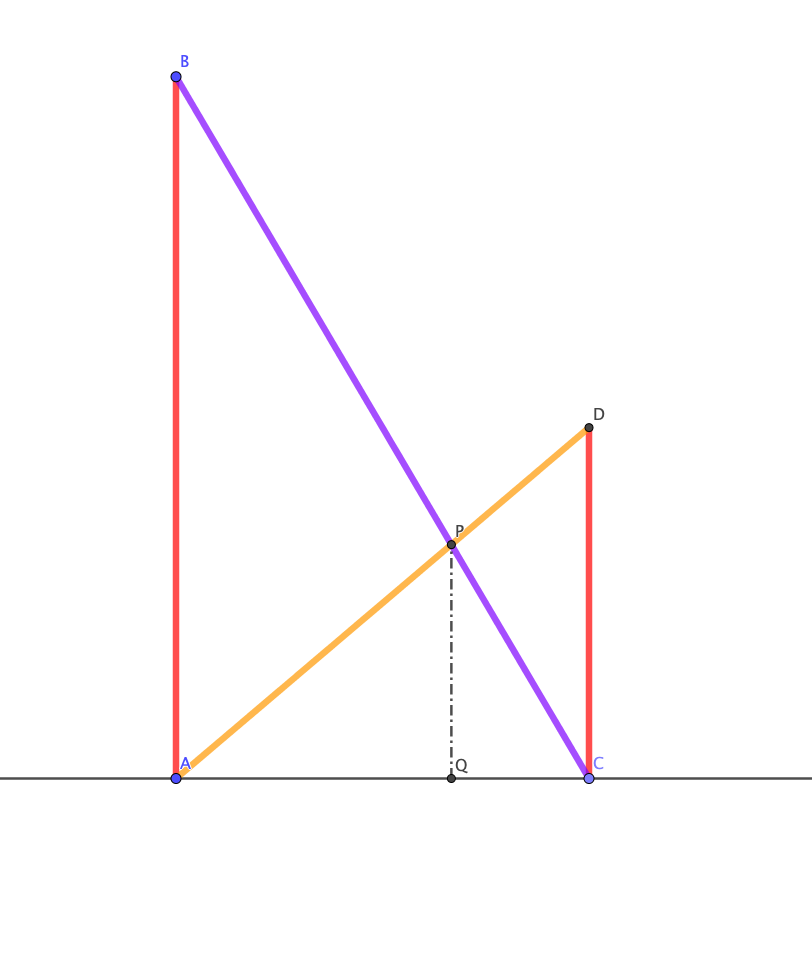
On trace la parallèle à la longueur du rectangle, passant par A , puis celle passant par C, puis la perpendiculaire à ces deux droites passant par B. Enfin on trace les segments [AB] et [BC] qui passent par les points ou sont tangents les cercles.
On obtient alors deux triangles rectangles AKB et BHC dont les hypothénuses [AB] et [BC] mesurent 1+4=5 et 4+2=6.
D’autre part la longueur BK est égale à la différence des rayons des cercles de centres respectifs B et A. Donc BK= 4-1=3
La longueur BH est égale à la différence des rayons des cercles de centres respectifs B et C. Donc BH=4-2=2
On applique le théorème de Pythagore dans le triangle ABK :
\(AK^2+BK^2=AB^2\) donc \(AK^2=AB^2-BK^2=5^2-3^2=16\). Donc \(AK=4\)
On applique le théorème de Pythagore dans le triangle BHC :
\(BH^2+HC^2=BC^2\) donc \(HC^2=BC^2-BH^2=6^2-2^2=32\) donc
\(HC=\sqrt{32}=4\sqrt{2}\)
Si on désigne par \(R_1\) et \(R_3\) les rayons des cercles de centres A et C, par L la longueur du rectangle, on a alors :
\(L=R_1+AK+HC+R_3=1+4+4\sqrt{2}+2=7+4\sqrt{2}\)