Enoncé du problème n° 55

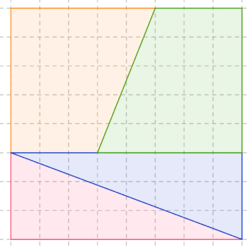
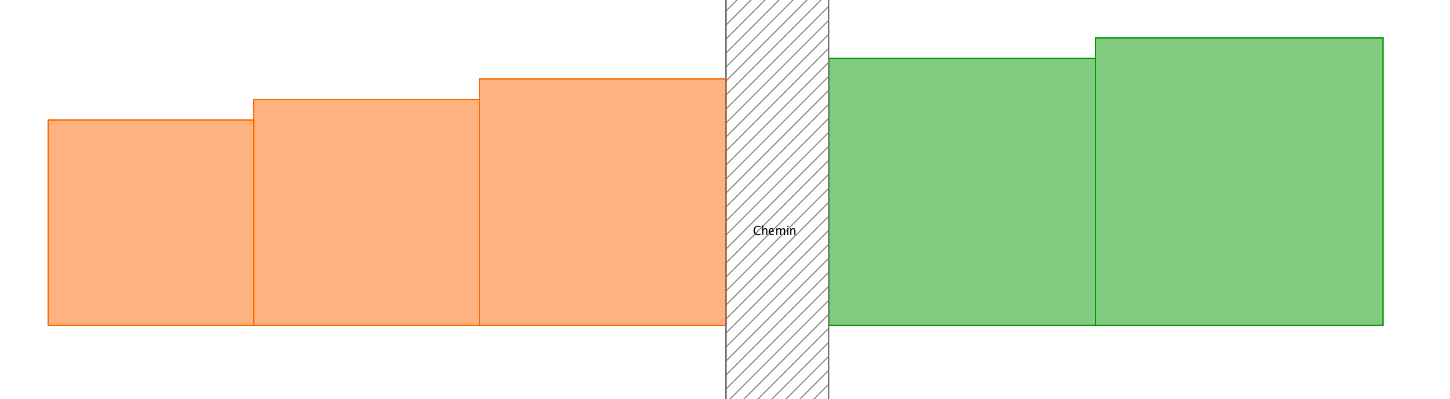
Observer et expliquer ce phénomène !
Correction du problème n° 55
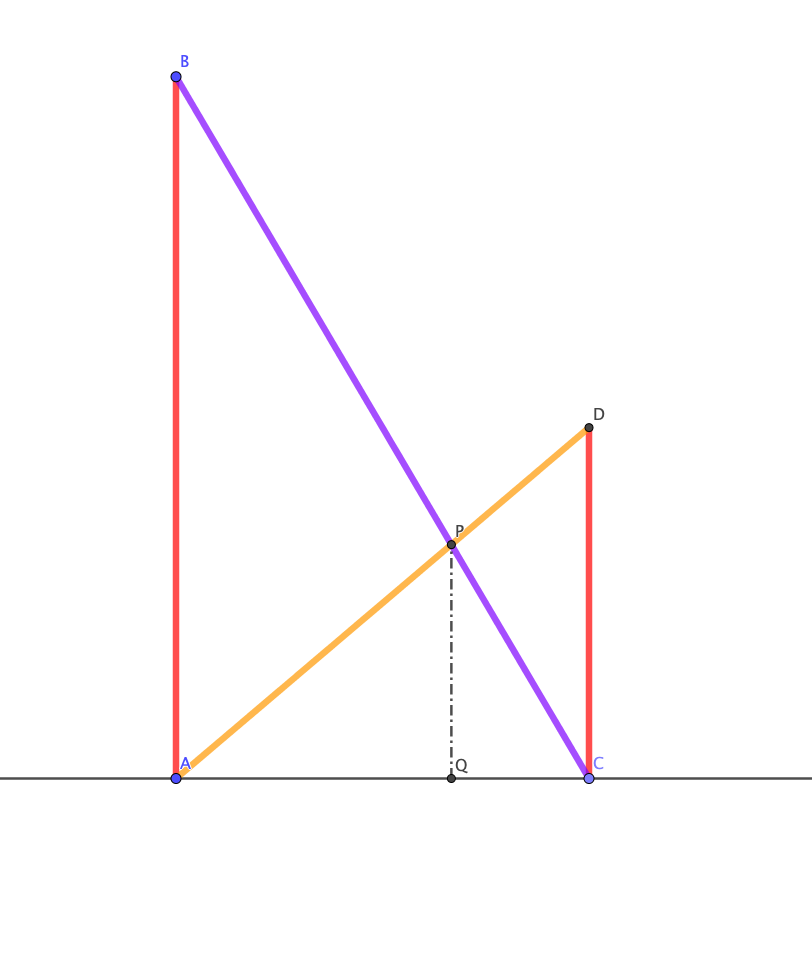
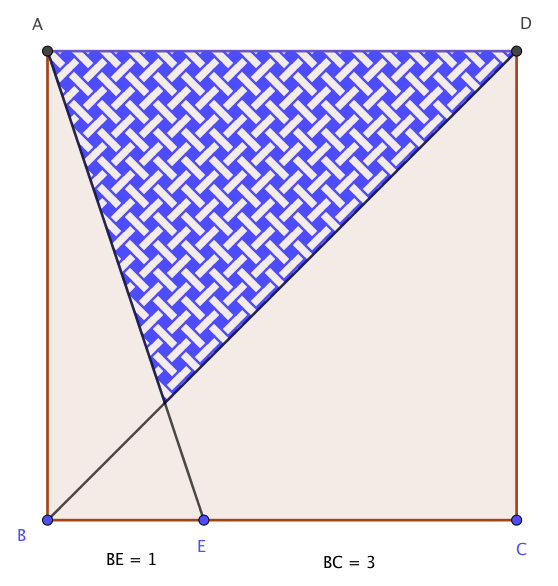
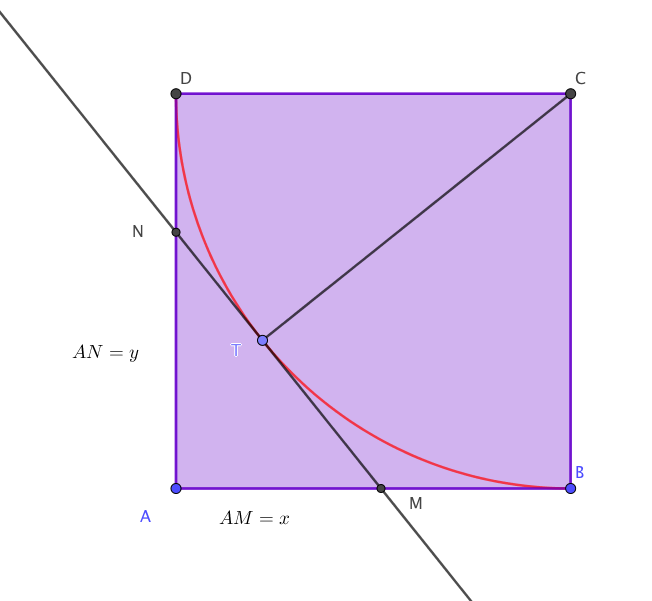
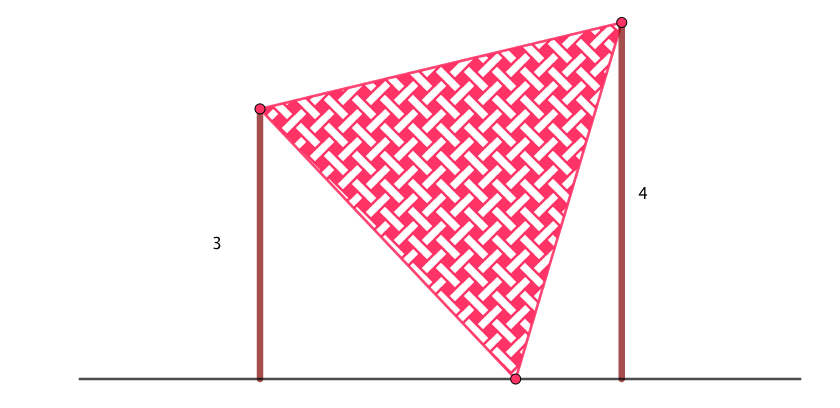
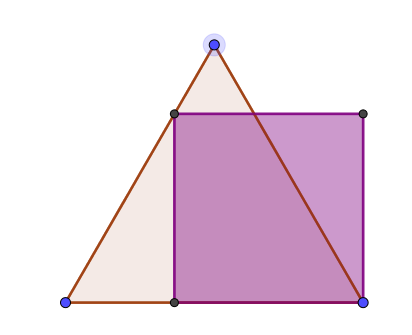
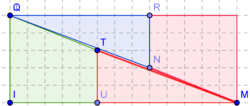
- On peut utiliser la figure jointe ( fichier Geogebra).
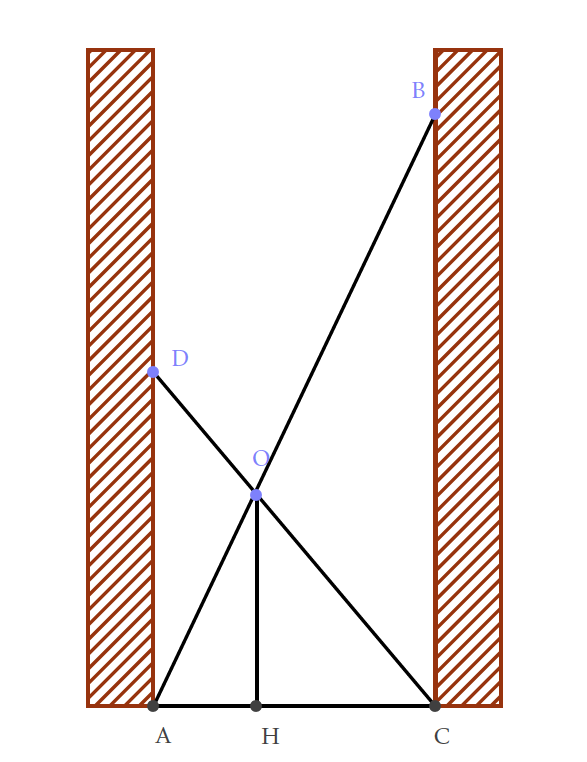
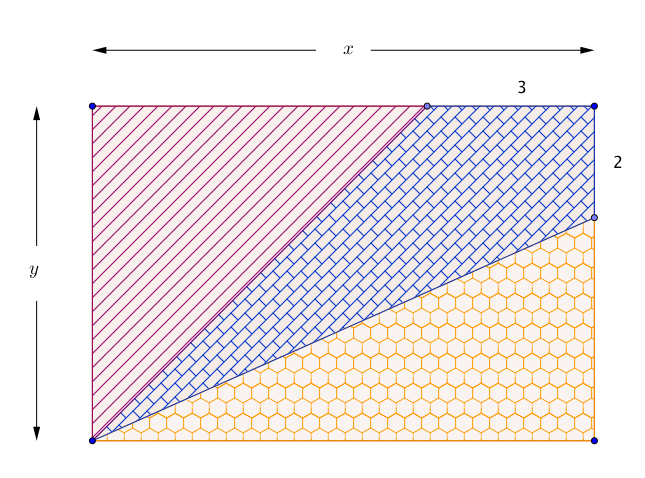
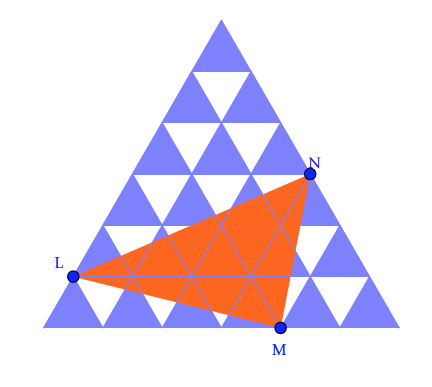
En zoomant, on remarque que \(O,U\) et \(R\) ne sont pas alignés !- \(O \begin{pmatrix} 0\\ 5\\ \end{pmatrix} ,U \begin{pmatrix} 8\\ 2\\ \end{pmatrix} \) et \(R \begin{pmatrix} 13\\ 0\\ \end{pmatrix} \)
- \(\vec{OU} \begin{pmatrix} 8\\ -3\\ \end{pmatrix} \) et \(\vec{OU} \begin{pmatrix} 13\\ -5\\ \end{pmatrix} \) et on montre que ces deux vecteurs ne sont pas colinéairres...
- Si les poins \(Q,U\) et \(R\) sont alignés, alors $$\tan \alpha =\dfrac{2}{5}=\dfrac{3}{8}\cdots$$ Or $$\dfrac{2}{5}\neq\dfrac{3}{8} $$ d'où la contradiction !