Une place rectangulaire de 24 mètres par 45 mètres est pavée par des carrés de 30 cm de côté, disposés comme sur un damier.
Une ficelle est tendue au sol entre deux coins opposés de la place (et il n’y a aucun obstacle).
Au-dessus de combien de carrés la ficelle passe-t-elle ?
La place est recouverte par 80 x 150 carrés.
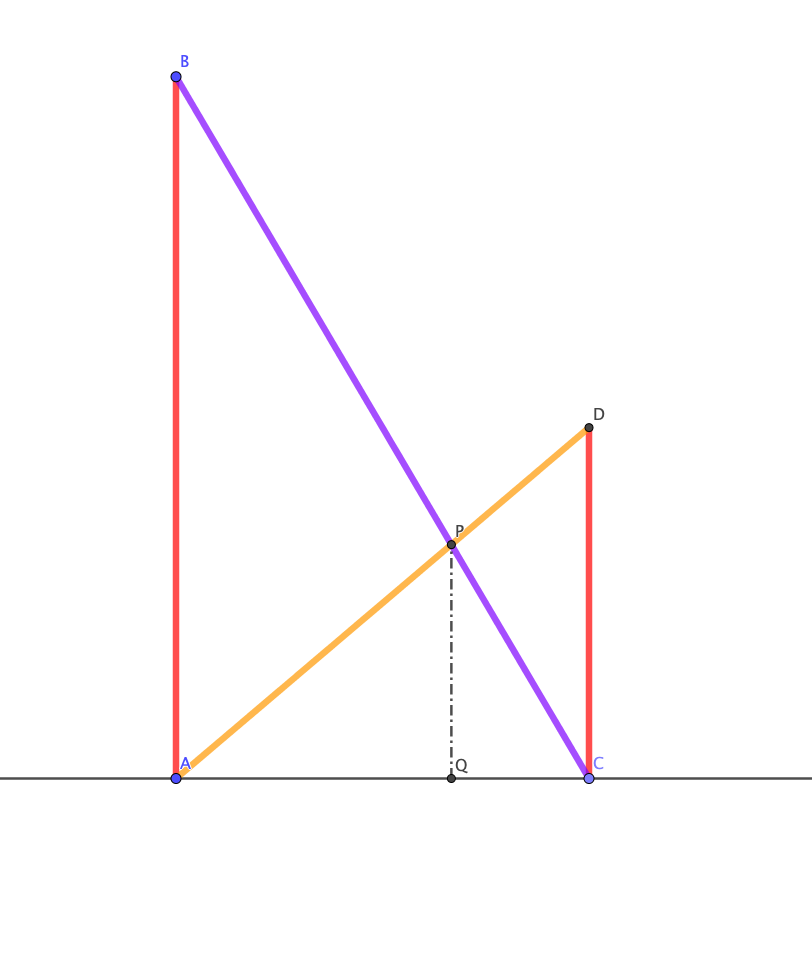
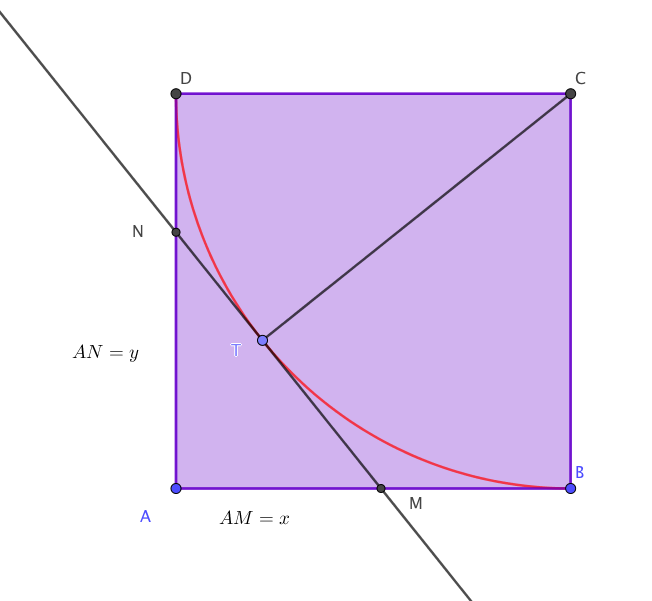
Modélisation : dans un repère orthogonal d’origine A, plaçons le point B(150 ; 0) et le point D(0 ; 80). Construisons le rectangle ABCD, de dimensions 150 et 80. Ce rectangle représente la place, et une unité représente le côté d’un des carrés pavant la place.
La ficelle peut alors être modélisée par \textcolor{blue}{[AC].} 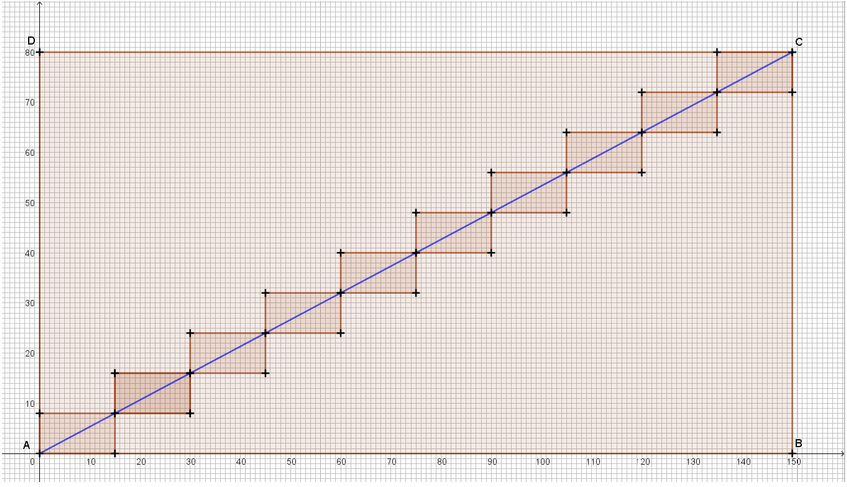
Sur ce graphique, chaque petit carré représente un carré du pavage.
\((AC)\) a pour équation : \(y=80/150 x\) soit \(y=8/15 x\)
On en déduit que le premier point à coordonnées entières appartenant au segment [AC], après A, a pour abscisse 15 et pour ordonnée 8.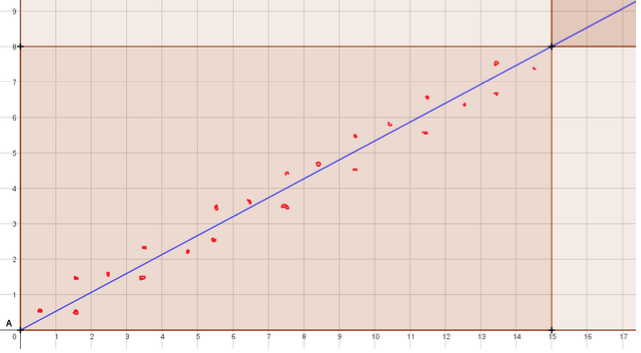
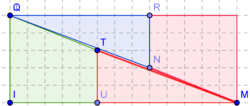
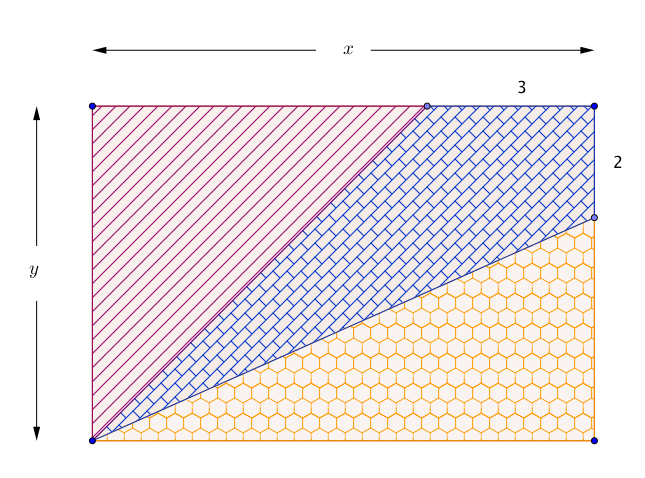
[AC] traverse donc, en diagonale, 10 rectangles de dimensions 15 et 8 unités.
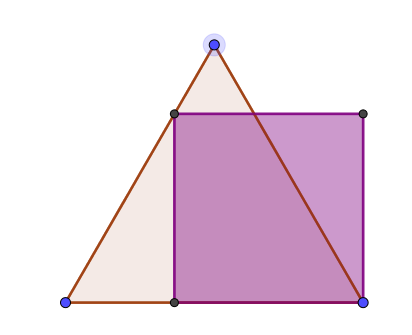
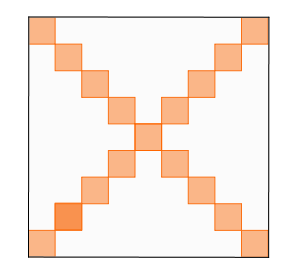
Zoomons sur l’un de ces rectangles et marquons d’un point rouge les carrés traversés par [AC] : on en compte 22.
Conclusion : La ficelle passe au-dessus de 220 carrés