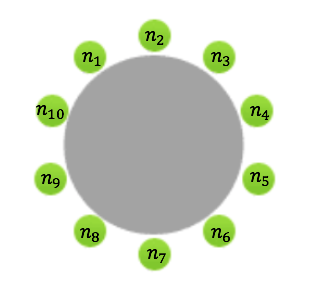
Dix personnes sont assises autour d’une table. Chacune pense à un nombre et le dit à ses deux voisins. Puis chaque personne dit à voix haute la moyenne des nombres de ses deux voisins.
Si les nombres de 1 à 10, dans cet ordre, ont été annoncés, à quel nombre la personne qui a dit 6 a-t-elle pensé ?
Notons \(n_1 , n_2 ,\cdots,n_9 \) et \(n_10 \) les nombres auxquels ont pensé les personnes qui ont respectivement annoncé \(1, 2, \cdots , 9 \) et 10. Il s’agit donc de déterminer \(n_6 \).
On a :
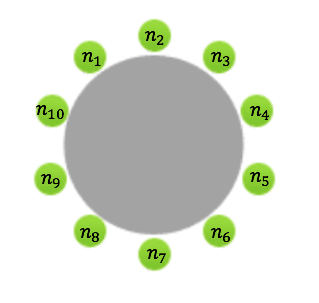
$$\left\lbrace \begin{array}{rl} \frac{n_{10}+n_2}{2}& =1\\ \frac{n_{1}+n_3}{2}& =2\\ \frac{n_{2}+n_4}{2}& =3\\ \frac{n_{3}+n_5}{2}& =4\\ \frac{n_{4}+n_6}{2}& =5\\ \frac{n_{5}+n_7}{2}& =6\\ \frac{n_{6}+n_8}{2}& =7\\ \frac{n_{7}+n_9}{2}& =8\\ \frac{n_{8}+n_{10}}{2}& =9\\ \frac{n_{9}+n_{1}}{2}& =10\\ \end{array} \right. \textbf{ soit } \left\lbrace \begin{array}{rl} n_{10}+n_2& =2\\ n_{1}+n_3& =4\\ n_{2}+n_4& =6\\ n_{3}+n_5& =8\\ n_{4}+n_6& =10\\ n_{5}+n_7& =12\\ n_{6}+n_8& =14\\ n_{7}+n_9& =16\\ n_{8}+n_{10}& =18\\ n_{9}+n_{1}& =20\\ \end{array} \right. $$ L’égalité \(n_4+n_6=10\) donne \(n_6=10-n_4 \);
puis, comme \(n_2+n_4=6, n_6=10-(6-n_2) \) , soit \(n_6=4+n_2\) ;
ensuite, comme \(n_{10}+n_2=2, n_6=4+(2- n_{10}) \), soit \(n_6=6-n_{10} \) ;
on continue de la même façon :
comme \(n_8+ n_{10}=18, n_6=6-(18-n_8) \) , soit \(n_6=-12+n_8\) ;
et enfin, comme \(n_6+n_8=14, n_6=-12+(14-n_6) \) , soit \(2n_6=2\) , puis \(n_6=1\).
La personne qui a dit 6 avait pensé au nombre 1.