Enoncé du problème n° 90
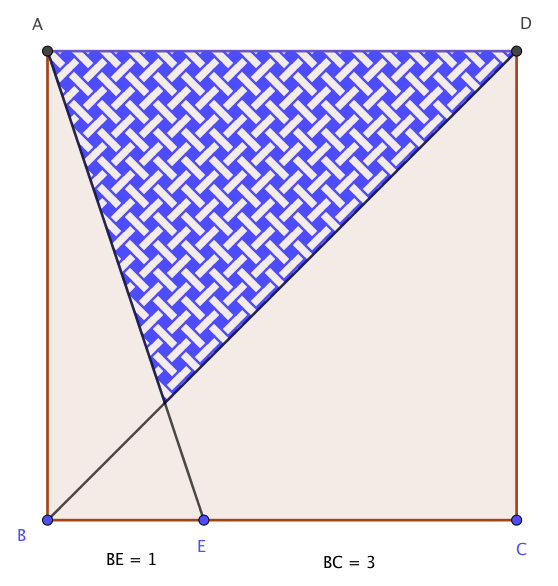

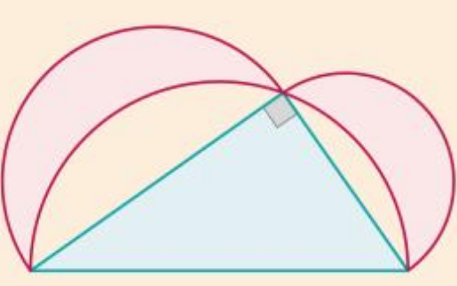
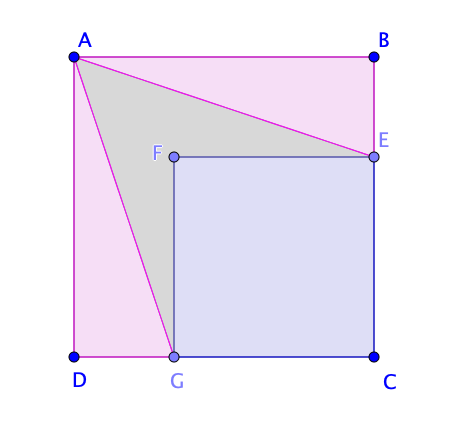
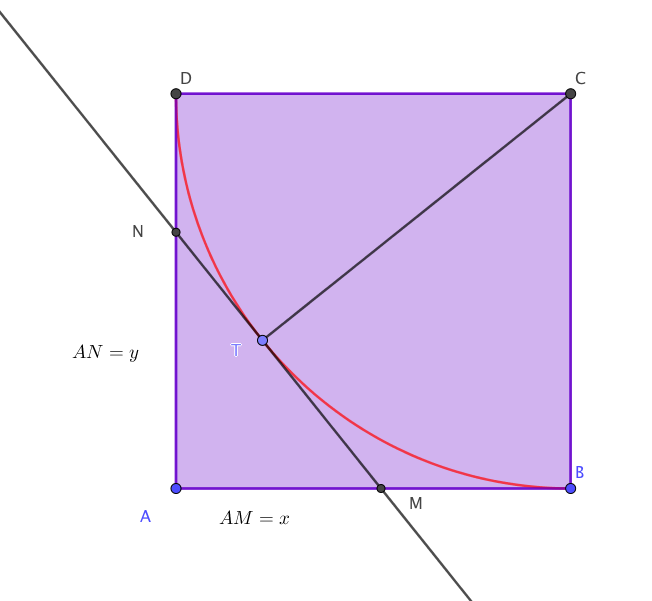
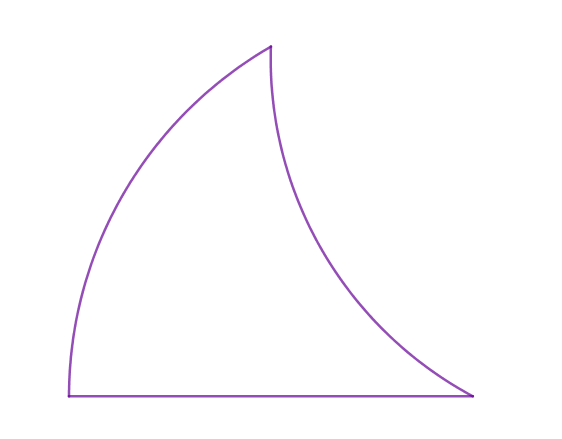
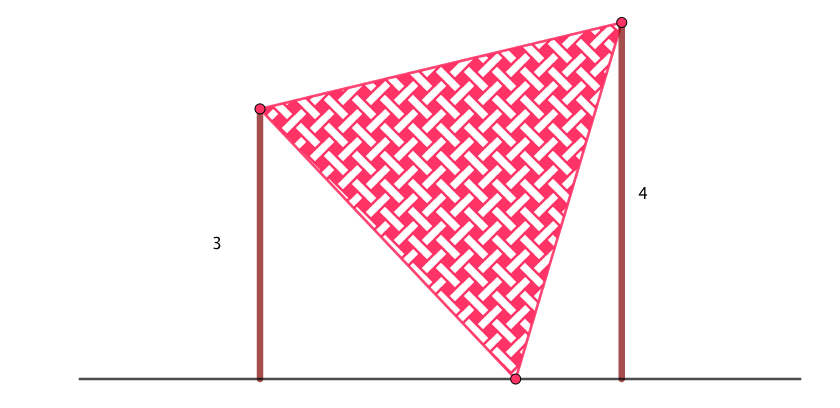
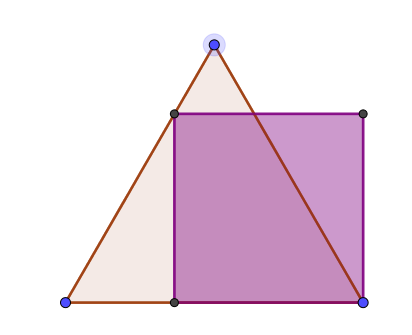
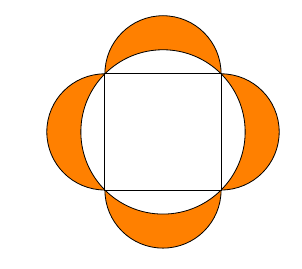
Si ABCD est un carré de côté 3 cm, quelle est l'aire de la région coloriée ?
Correction du problème n° 90
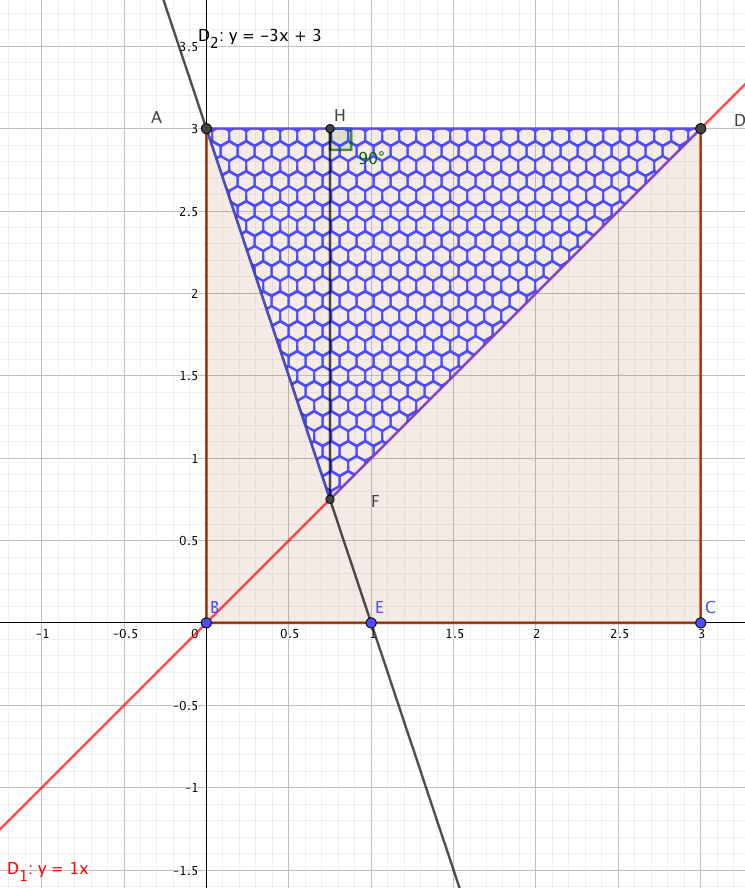

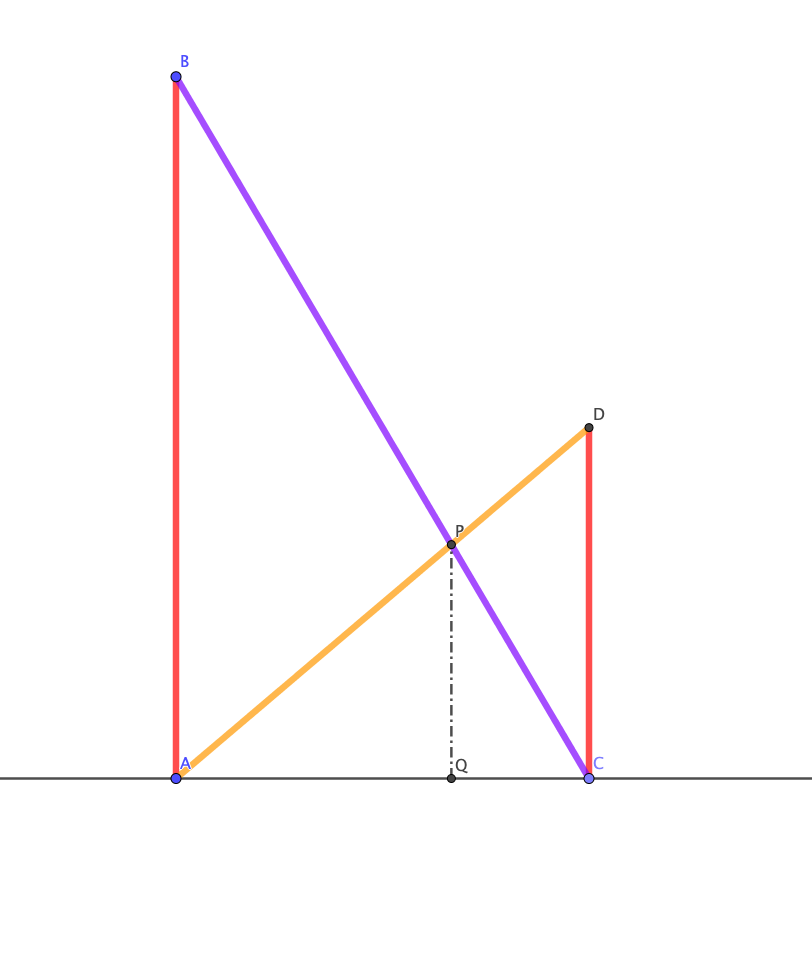
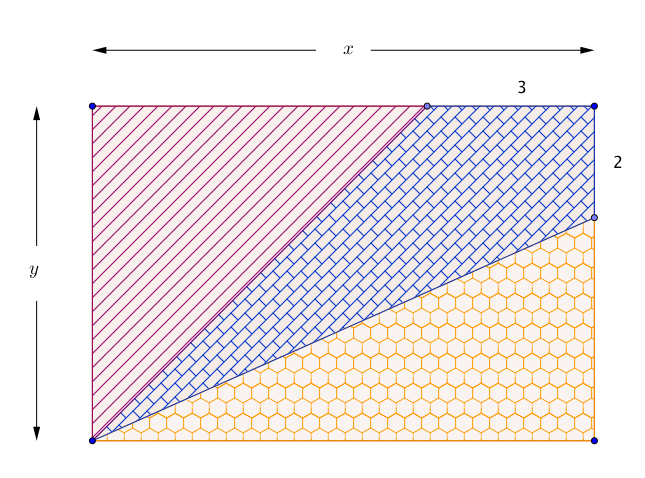
Avec les notations de la figure ci-dessus, l'aire du triangle FAD vaut : $\mathcal{A}= \dfrac{AD\times FH}{2}= \dfrac{3}{2}FH$.
Calculons alors les cooronnées de $H$, point se trouvant à l'intersection des droites $(BD)$ et $(AE)$.
Calculons alors les cooronnées de $H$, point se trouvant à l'intersection des droites $(BD)$ et $(AE)$.
- Equation de $(BD)$:
cette droite passe par l'origine O et a pour coeffifficient directeur 1.
Ainsi (BD): $y=x$ - Equation de $(AE)$:
son coefficient directer est -3.
et a pour équation réduite : $y-y_A= m(x-x_A)$, soit $y-3=-3(x-0)$
Ainsi (AE): $y=-3x+3$ - Coordonnées de H: $$\left\lbrace \begin{array}{l} y=x\\ y=-3x+3 \end{array} \right.\iff \left\lbrace \begin{array}{l} y=x\\ x=-3x+3 \end{array} \right. \iff \left\lbrace \begin{array}{l} y=x\\ x=\frac{3}{4} \end{array} \right.\iff \left\lbrace \begin{array}{l} y=\frac{3}{4}\\ x=\frac{3}{4} \end{array} \right.$$ Ainsi $H\left( \dfrac{3}{4}; \dfrac{3}{4}\right) $.
- Alors $FH= 3- \dfrac{3}{4}= \dfrac{9}{4}$, puis l'aire coloriée vaut $\mathcal{A}= \dfrac{3}{2}\times \dfrac{9}{4}= \dfrac{27}{8} $.
Conclusion : l'aire coloriée vaut donc $3,375 cm^2$