Enoncé du problème n° 105
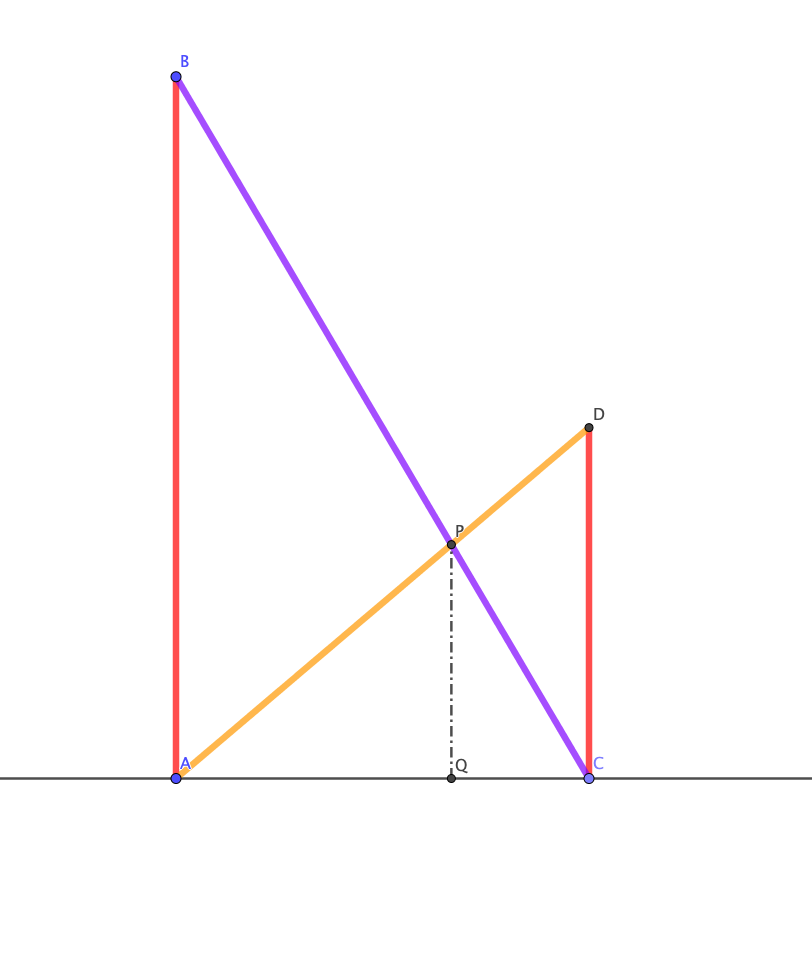

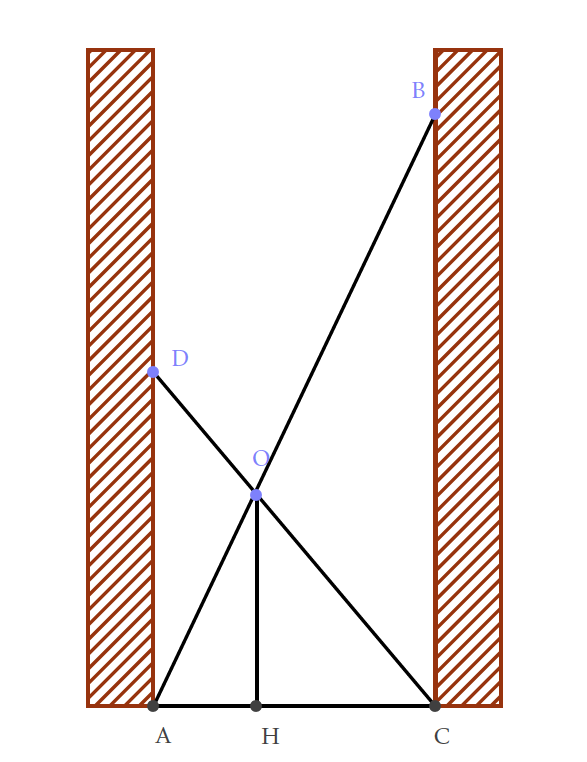
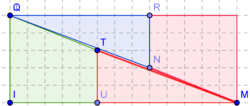
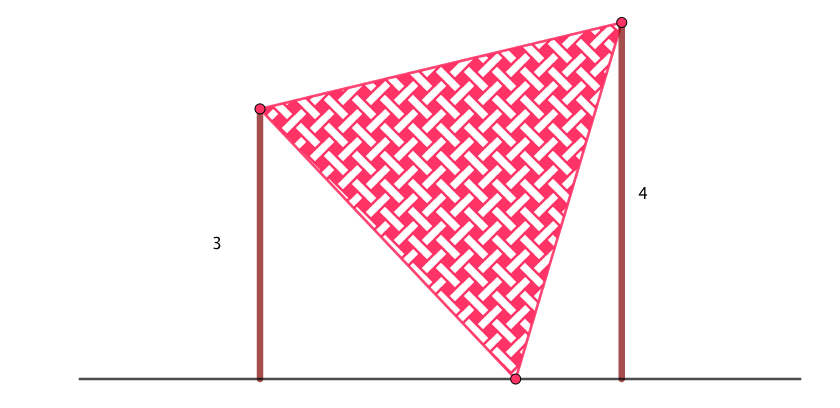
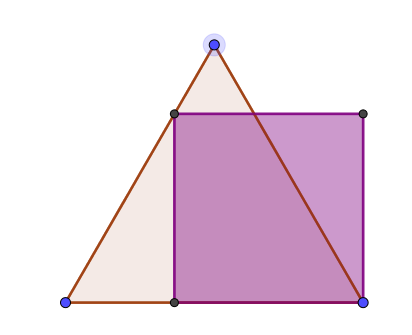
$AB$ et $CD$ sont deux pièces de bois verticales sur une surface horizontale $AC$.
$AD$ est un élastique qui peut être étiré théoriquement aussi loin que vous le souhaitez.
$BC$ est plus long que $AD$, mais possède les mêmes propriétés.
$P$ est le point d'intersection des deux élastiques.
Démontrez que la hauteur $P$ au-dessus de la surface horizontale reste constante peu importe la longueur $AC$ (en supposant que les élastiques restent tendus).
Dans l'exemple ci-dessus, $AB =$12 cm et $CD =$ 6 cm et je pourrais vous demander la distance constante $PQ$, peu importe la distance que mesure $AC$.
Correction du problème n° 105
Une solution :
On se place dans le repère où
On se place dans le repère où
- $A(0,0); B(0,12);C(a,0),D(a,6)$
- on calcule les coordonnées du point $P$ intersection des droites $(AD)$ et $(BC)$.
On obtient $(AD): y=\frac{6}{a}x$ et $(BC): y=-\frac{12}{a}x+12$ - On résout le système $\left\lbrace \begin{array}{l} y=\frac{6}{a}x\\ y=-\frac{12}{a}x+12 \end{array} \right. \iff \left\lbrace \begin{array}{l} y=\frac{6}{a}x\\ \frac{6}{a}x=-\frac{12}{a}x+12 \end{array} \right. \iff \left\lbrace \begin{array}{l} y=\frac{6}{a}\times \frac{ 2}{3}a =4\\ x= \frac{ 2}{3}a \end{array} \right. $
- On a donc $P( \frac{ 2}{3}a;4)$ et $Q( \frac{ 2}{3}a;0)$ et donc $PQ=4$