Enoncé du problème n° 111
On note $M_0 $le mot $ab$ et pour tout entier naturel $n$, le mot $M_{n+1}$ se construit à partir du mot $M_n$ en remplaçant tous les $a$ par $ab$ et tous les $b$ par $bab$.
Ainsi, $M_0 = ab$, $M_1 = abbab$ et $M_2 = abbabbababbab$.
- Quelle est la longueur du mot M10 ?
- Combien de b contient le mot M10 ?
Correction du problème n° 111
On note $a_n$ et $b_n$ respectivement le nombre de $a$ et de $b$ dans le mot $M_n$ .
On a : $a_0=1$,$a_1=2,a_2=5$
$b_0=1,b_1=3,b_2=8$
Chaque $a$ dans $M_n$ va être remplacé par $ab$ dans $M_{n+1}$ donc va "engendrer" un seul $a$.
Chaque $b$ dans Mn va être remplacé par $bab$ dans $M_{n+1}$ donc va "engendrer" un seul $a$.
Donc $a_{n+1}=a_n+b_n$
Chaque $a$ dans $M_n$ va être remplacé par $ab$ dans $M_{n+1}$ donc va "engendrer" un seul $b$.
Chaque $b$ dans $M_n$ va être remplacé par $bab$ dans $M_{n+1}$ donc va "engendrer" un $b$ de plus.
Donc $b_{n+1}=a_n+2 b_n$.
Si on note $L_n$ la longueur du mot $M_n$ , on a : $L_n=a_n+b_n$.
En effectuant les calculs de proche en proche, on peut facilement trouver $a_10,b_10 $ et $L_10$.
Par exemple :
$a_3=a_2+b_2=5+8=13$
$b_3=a_2+2b_2=5+2\times 8=21$
$a_4=a_3+b_3=13+21=34$
$b_4=a_3+2b_3=13+2\times 21=55$
etc.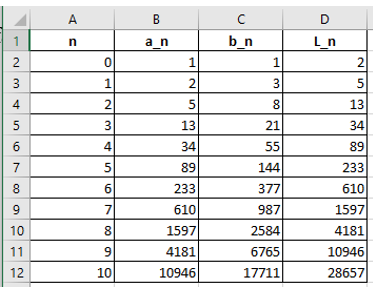
Les formules à taper sont :
Dans A2 : 0, Dans B2 : 1, Dans C2 : 1 Dans D2 : = B2 + C2
Dans A3 : = A2 + 1, Dans B3 : = B2 + C2, Dans C3 : = B2 + 2*C2, Dans D3 : = B3 + C3.
Ensuite, on sélectionne les quatre cellules de A3 à D3, et on fait un "recopier vers le bas", jusqu'à la ligne 12 pour obtenir $a_{10},b_{10}$ et $L_{10}$.
On lit : La longueur du mot $M_{10}$ est $L_{10}=28657$ et il contient 17711 caractères $b$ ( $b_{10}=17711$ ).

Voilà ce que donne l'exécution du programme pour n = 3 et pour n = 10. On voit que le mot M10 n'est pas écrit car il prend 359 lignes ‼!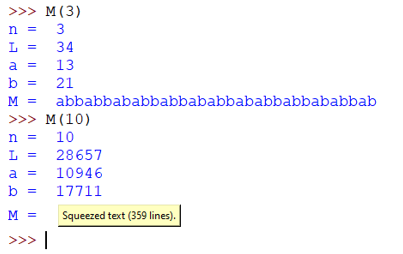
Enfin, pour aller plus loin, il est possible d'obtenir la valeur de $a_n$ et de $b_n$ donc de $L_n$ en fonction de $n$ directement. En effet, on peut se rendre compte facilement en regardant l'écran du tableur précédent que les $a_n$ sont les termes de rangs impairs de la célèbre suite de Fibonacci et les $b_n$ en sont les termes de rangs pairs (à partir de 2).
Pour rappel, la suite de Fibonacci, est la suite $(F_n )$ définie, pour tout entier naturel $n$ par : $F_0=0 , F_1=1$ et $F_{n+2}=F_{n+1}+F_n$ .
On a :
$ F_1=1=a_0$
$F_2=1=b_0$
$F_3=2=a_1$
$F_4=3=b_1$
$F_5=5=a_2$
$F_6=8=b_2$
etc.
Ainsi : $a_n=F_{2n+1}$ et $b_n=F_{2n+2}$ pour tout entier $n \geq 0$.
On peut trouver facilement sur Wikipédia par exemple, que :
$F_n=\dfrac{1}{\sqrt 5}\times \left(\varphi^n- \varphi ' ^n \right)$ avec $\varphi=\dfrac{1+\sqrt 5}{2} $ et $\varphi '=\dfrac{1-\sqrt 5}{2} $ ( $\varphi$ est le célèbre Nombre d'Or ).
Donc : $a_n=\dfrac{1}{\sqrt 5} \left(\varphi^{2n+1}-\varphi '^{2n+1}\right )$ et $b_n=\dfrac{1}{\sqrt 5} \left(\varphi^{2n+1}-\varphi '^{2n+1}\right )$.
On peut alors créer un programme Python qui calcule directement $a_n,b_n$ et $L_n$ :

Voilà ce que donne l'exécution du programme pour $n = 10$.

On a : $a_0=1$,$a_1=2,a_2=5$
$b_0=1,b_1=3,b_2=8$
Chaque $a$ dans $M_n$ va être remplacé par $ab$ dans $M_{n+1}$ donc va "engendrer" un seul $a$.
Chaque $b$ dans Mn va être remplacé par $bab$ dans $M_{n+1}$ donc va "engendrer" un seul $a$.
Donc $a_{n+1}=a_n+b_n$
Chaque $a$ dans $M_n$ va être remplacé par $ab$ dans $M_{n+1}$ donc va "engendrer" un seul $b$.
Chaque $b$ dans $M_n$ va être remplacé par $bab$ dans $M_{n+1}$ donc va "engendrer" un $b$ de plus.
Donc $b_{n+1}=a_n+2 b_n$.
Si on note $L_n$ la longueur du mot $M_n$ , on a : $L_n=a_n+b_n$.
En effectuant les calculs de proche en proche, on peut facilement trouver $a_10,b_10 $ et $L_10$.
Par exemple :
$a_3=a_2+b_2=5+8=13$
$b_3=a_2+2b_2=5+2\times 8=21$
$a_4=a_3+b_3=13+21=34$
$b_4=a_3+2b_3=13+2\times 21=55$
etc.
Pour accélérer les calculs, on peut utiliser un tableur :

Les formules à taper sont :
Dans A2 : 0, Dans B2 : 1, Dans C2 : 1 Dans D2 : = B2 + C2
Dans A3 : = A2 + 1, Dans B3 : = B2 + C2, Dans C3 : = B2 + 2*C2, Dans D3 : = B3 + C3.
Ensuite, on sélectionne les quatre cellules de A3 à D3, et on fait un "recopier vers le bas", jusqu'à la ligne 12 pour obtenir $a_{10},b_{10}$ et $L_{10}$.
On lit : La longueur du mot $M_{10}$ est $L_{10}=28657$ et il contient 17711 caractères $b$ ( $b_{10}=17711$ ).
On peut aussi faire un programme Python
qui produit vraiment les différents mots $M_n$ et compte le nombre de $a$ et le nombre de $b$, et en déduit le nombre total de caractères.
Voilà ce que donne l'exécution du programme pour n = 3 et pour n = 10. On voit que le mot M10 n'est pas écrit car il prend 359 lignes ‼!

Enfin, pour aller plus loin, il est possible d'obtenir la valeur de $a_n$ et de $b_n$ donc de $L_n$ en fonction de $n$ directement. En effet, on peut se rendre compte facilement en regardant l'écran du tableur précédent que les $a_n$ sont les termes de rangs impairs de la célèbre suite de Fibonacci et les $b_n$ en sont les termes de rangs pairs (à partir de 2).
Pour rappel, la suite de Fibonacci, est la suite $(F_n )$ définie, pour tout entier naturel $n$ par : $F_0=0 , F_1=1$ et $F_{n+2}=F_{n+1}+F_n$ .
On a :
$ F_1=1=a_0$
$F_2=1=b_0$
$F_3=2=a_1$
$F_4=3=b_1$
$F_5=5=a_2$
$F_6=8=b_2$
etc.
Ainsi : $a_n=F_{2n+1}$ et $b_n=F_{2n+2}$ pour tout entier $n \geq 0$.
On peut trouver facilement sur Wikipédia par exemple, que :
$F_n=\dfrac{1}{\sqrt 5}\times \left(\varphi^n- \varphi ' ^n \right)$ avec $\varphi=\dfrac{1+\sqrt 5}{2} $ et $\varphi '=\dfrac{1-\sqrt 5}{2} $ ( $\varphi$ est le célèbre Nombre d'Or ).
Donc : $a_n=\dfrac{1}{\sqrt 5} \left(\varphi^{2n+1}-\varphi '^{2n+1}\right )$ et $b_n=\dfrac{1}{\sqrt 5} \left(\varphi^{2n+1}-\varphi '^{2n+1}\right )$.
On peut alors créer un programme Python qui calcule directement $a_n,b_n$ et $L_n$ :

Voilà ce que donne l'exécution du programme pour $n = 10$.